题目内容
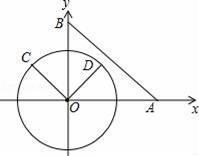
在平面直角坐标xOy中,已知点A(6,0),点B(0,6),动点C在以半径为3的⊙O上,连接OC,过O点作OD⊥OC,OD与⊙O相交于点D(其中点C、O、D按逆时针方向排列),连接AB.
(1)当OC∥AB时,∠BOC的度数为 ;
(2)连接AC,BC,在点C在⊙O运动过程中,△ABC的面积是否存在最大值?并求出△ABC的最大值;
(3)直接写出在(2)的条件下D点的坐标.

【考点】圆的综合题.
【分析】(1)根据点A和点B坐标易得△OAB为等腰直角三角形,则∠OBA=45°,由于OC∥AB,所以当C点在y轴左侧时,有∠BOC=∠OBA=45°;当C点在y轴右侧时,有∠BOC=180°﹣∠OBA=135°,从而得出答案;
(2)由△OAB为等腰直角三角形得AB=
 OA,根据三角形面积公式得到当点C到AB的距离最大时,△ABC的面积最大,过O点作OE⊥AB于E,OE的反向延长线交⊙O于C,此时C点到AB的距离的最大值为CE的长,然后利用等腰直角三角形的性质计算出OE,然后计算△ABC的面积;
OA,根据三角形面积公式得到当点C到AB的距离最大时,△ABC的面积最大,过O点作OE⊥AB于E,OE的反向延长线交⊙O于C,此时C点到AB的距离的最大值为CE的长,然后利用等腰直角三角形的性质计算出OE,然后计算△ABC的面积;
(3)由(2)可知当△ABC的面积最大值时,则点C在第三象限,因为OD⊥OC,所以点D在第二象限,过点D作DH⊥OB,DM⊥AO,分别求出DH,DM的长即可求出点D的坐标.
【解答】解:(1)∵点A(6,0),点B(0,6),
∴OA=OB=6,
∴△OAB为等腰直角三角形,
∴∠OBA=45°,
∵OC∥AB,
∴当C点在y轴左侧时,∠BOC=∠OBA=45°,
当C点在y轴右侧时,∠BOC=180°﹣∠OBA=135°,
∴∠OBA=45°或135°;
故答案为:45°或135°;
(2)∵△OAB为等腰直角三角形,
∴AB=
 OA=6
OA=6
 ,
,
∴当点C到AB的距离最大时,△ABC的面积最大,
过O点作OE⊥AB于E,OE的反向延长线交⊙O于C,
如图:此时C点到AB的距离最大值为CE的长,
∵△OAB为等腰直角三角形,
∴OE=
 AB=3
AB=3
 ,
,
∴CE=OC+OE=3+3
 ,△ABC的面积=
,△ABC的面积=
 CE•AB=
CE•AB=
 (3+3
(3+3
 )×6
)×6
 =9
=9
 +18,
+18,
当点C在⊙O上运动到第三象限的角平分线与圆的交点位置时,△ABC的面积最大,最大值为9
 +18.
+18.
(3)过点D作DH⊥OB,DM⊥AO,
由(2)可知点C在⊙O上运动到第三象限的角平分线与圆的交点位置,
∴∠COM=45°,
∵OD⊥OC,
∴∠DOM=45°,
∵OD=3,
∴DM=
 ,DH=
,DH=
 ,
,
∴点D坐标是(﹣
 ,
,
 ).
).


【点评】本题考查了圆的综合题,用到的知识点是平行线的性质和等腰直角三角形的判定与性质;熟练运用勾股定理进行几何计算是本题的关键.




 B.
B.






 B.
B.
 C.
C.
 D.
D.


 ,下列结论不正确的是( )
,下列结论不正确的是( ) B.
B. C.
C. D.
D.