Question

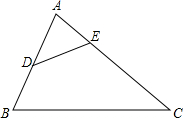如图，点D、E分别为AB、AC边上两点，且AD=4，BD=2，AE=2，CE=10．
试说明：（1）△ADE∽△ACB；（2）若BC=9，求DE的长．

Answer 1

考点：相似三角形的判定与性质

专题：

分析：（1）由条件可得

AE

AB

=

AD

AC

，且∠A为公共角，则可证明△ADE∽△ACB；
（2）由（1）△ADE∽△ACB可得

DE

BC

=

1

3

，可求得DE．

解答：解：（1）∵AD=4，BD=2，AE=2，CE=10，
∴AB=6，AC=12，
∴

AE

AB

=

1

3

=

AD

AC

，
∵∠A=∠A，
∴△ADE∽△ACB；
（2）∵△ADE∽△ACB，
∴

DE

BC

=

AD

AC

=

1

3

，
∵BC=9，
∴DE=3．

点评：本题主要考查相似三角形的判定和性质，掌握三角形相似的判定方法，即有两组角对应相等、两组对应边的比相等且夹角相等或三组对应边的比相等是解题的关键．