题目内容
已知抛物线y=(m-1)x2+(m-2)x-1.
(1)当m为何值时,抛物线与x轴有两个交点?
(2)若抛物线与x轴交于A、B两点,与y轴交于C(0,-1),且S△ABC=2,求m的值.
(1)当m为何值时,抛物线与x轴有两个交点?
(2)若抛物线与x轴交于A、B两点,与y轴交于C(0,-1),且S△ABC=2,求m的值.
考点:抛物线与x轴的交点
专题:
分析:(1)根据二次函数与一元二次方程的关系,将抛物线与x轴的交点问题转化为根的判别式,列出不等式解答.
(2)利用根与系数的关系求得线段AB的长度,然后由三角形的面积公式列出关于m的方程,通过解放方程求得m的值.
(2)利用根与系数的关系求得线段AB的长度,然后由三角形的面积公式列出关于m的方程,通过解放方程求得m的值.
解答:解:(1)∵抛物线与x轴有两个交点,
∴△>0,且m-1≠0,
∴(m-2)2-4×(m-1)(-1)>0且m≠1,
整理得m2>0且m≠1,
解得m≠0且m≠1.
故m≠0且m≠1时,抛物线与x轴有两个交点;
(2)设A(a,0),B(b,0).则
a+b=
,ab=
.
则AB=|a-b|=
=
=|
|
所以
AB•OC=
×|
|×1=2,
解得 m=
或m=
.
∴△>0,且m-1≠0,
∴(m-2)2-4×(m-1)(-1)>0且m≠1,
整理得m2>0且m≠1,
解得m≠0且m≠1.
故m≠0且m≠1时,抛物线与x轴有两个交点;
(2)设A(a,0),B(b,0).则
a+b=
| 2-m |
| m-1 |
| 1 |
| 1-m |
则AB=|a-b|=
| (a+b)2-4ab |
(
|
| m |
| 1-m |
所以
| 1 |
| 2 |
| 1 |
| 2 |
| m |
| 1-m |
解得 m=
| 4 |
| 5 |
| 4 |
| 3 |
点评:此题考查了抛物线与x轴的交点,注意:二次函数与一元二次方程的关系,还考查了一元二次方程根的判别式,难度不大,是基础题.

练习册系列答案
相关题目
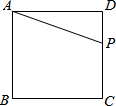 如图,正方形ABCD的边长为4,点P为CD上任意一点(不与C、D重合),设DP=x,四边形ABCP的面积为y.
如图,正方形ABCD的边长为4,点P为CD上任意一点(不与C、D重合),设DP=x,四边形ABCP的面积为y.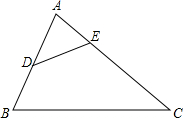 如图,点D、E分别为AB、AC边上两点,且AD=4,BD=2,AE=2,CE=10.
如图,点D、E分别为AB、AC边上两点,且AD=4,BD=2,AE=2,CE=10.