题目内容
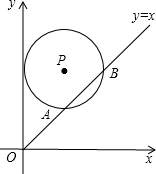 如图,在平面直角坐标系中,⊙P的圆心是(4,a)且(a>2)半径为4,函数y=x的图象被⊙P截得的弦AB的长为4
如图,在平面直角坐标系中,⊙P的圆心是(4,a)且(a>2)半径为4,函数y=x的图象被⊙P截得的弦AB的长为4| 3 |
考点:垂径定理,坐标与图形性质
专题:
分析:过P点作PE⊥AB于E,过P点作PC⊥x轴于C,交AB于D,连接PA.分别求出PD、DC,相加即可.
解答: 解:过P点作PE⊥AB于E,过P点作PC⊥x轴于C,交AB于D,连接PA.
解:过P点作PE⊥AB于E,过P点作PC⊥x轴于C,交AB于D,连接PA.
∵PE⊥AB,AB=4
,半径为4,
∴AE=
AB=2
,PA=4,
根据勾股定理得:PE=
=
=2,
∵点A在直线y=x上,
∴∠AOC=45°,
∵∠DCO=90°,
∴∠ODC=45°,
∴△OCD是等腰直角三角形,
∴OC=CD=4,
∴∠PDE=∠ODC=45°,
∴∠DPE=∠PDE=45°,
∴DE=PE=2,
∴PD=2
.
∵⊙P的圆心是(4,a),
∴a=PD+DC=4+2
.
故答案为4+2
.
 解:过P点作PE⊥AB于E,过P点作PC⊥x轴于C,交AB于D,连接PA.
解:过P点作PE⊥AB于E,过P点作PC⊥x轴于C,交AB于D,连接PA.∵PE⊥AB,AB=4
| 3 |
∴AE=
| 1 |
| 2 |
| 3 |
根据勾股定理得:PE=
| PA2-EA2 |
42-(2
|
∵点A在直线y=x上,
∴∠AOC=45°,
∵∠DCO=90°,
∴∠ODC=45°,
∴△OCD是等腰直角三角形,
∴OC=CD=4,
∴∠PDE=∠ODC=45°,
∴∠DPE=∠PDE=45°,
∴DE=PE=2,
∴PD=2
| 2 |
∵⊙P的圆心是(4,a),
∴a=PD+DC=4+2
| 2 |
故答案为4+2
| 2 |
点评:本题考查的是垂径定理,题中运用圆与直线的关系以及直角三角形等知识求出线段的长是解题的关键.注意函数y=x与x轴的夹角是45°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
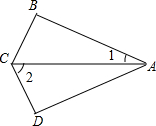 如图,将Rt△ABC沿直线AC翻折得到△ADC,其中∠B=90°,∠1=40°,则∠2=( )
如图,将Rt△ABC沿直线AC翻折得到△ADC,其中∠B=90°,∠1=40°,则∠2=( )| A、40° | B、50° |
| C、45° | D、60° |
同一平面内,半径分别为2cm和3cm的两圆相切,则这两圆的圆心距是( )
| A、5cm | B、1cm |
| C、5cm或1cm | D、4cm |
在下列四个图形中,能作为y是x的函数的图象的是( )
A、 |
B、 |
C、 |
D、 |
下列画图语句中正确的是( )
| A、画射线OP=5cm |
| B、画射线OA的反向延长线 |
| C、画出A、B两点的中点 |
| D、画出A、B两点的距离 |
 如图1所示,一只封闭的圆柱形容器内盛了一半水(容器的厚度忽略不计),圆柱形容器底面直径为高的2倍,现将该容器竖起后如图2所示,设图1、图2中水所形成的几何体的表面积分别为S1、S2,则S1与S2的大小关系是( )
如图1所示,一只封闭的圆柱形容器内盛了一半水(容器的厚度忽略不计),圆柱形容器底面直径为高的2倍,现将该容器竖起后如图2所示,设图1、图2中水所形成的几何体的表面积分别为S1、S2,则S1与S2的大小关系是( )| A、S1≤S2 |
| B、S1<S2 |
| C、S1>S2 |
| D、S1=S2 |