题目内容
一个不透明的布袋中装有4个只有颜色不同的球,其中1个黄球、1个蓝球、2个红球.
(1)求摸出一个球是黄球的概率;
(2)摸出1个球,记下颜色后不放回,再摸出1个球.求两次摸出的球恰好都是红球的概率(要求画树状图或列表);
(3)现再将n个黄球放入布袋,搅匀后,使摸出1个球是黄球的概率为
.求n的值.
(1)求摸出一个球是黄球的概率;
(2)摸出1个球,记下颜色后不放回,再摸出1个球.求两次摸出的球恰好都是红球的概率(要求画树状图或列表);
(3)现再将n个黄球放入布袋,搅匀后,使摸出1个球是黄球的概率为
| 5 |
| 8 |
考点:列表法与树状图法,概率公式
专题:计算题
分析:(1)直接根据概率公式求解;
(2)先利用树状图展示所有12种等可能的结果数,再找出两次摸出的球恰好都是红球的所占的结果数,然后根据概率公式求解;
(3)根据概率公式得到
=
,然后利用比例性质求解即可.
(2)先利用树状图展示所有12种等可能的结果数,再找出两次摸出的球恰好都是红球的所占的结果数,然后根据概率公式求解;
(3)根据概率公式得到
| 1+n |
| n+4 |
| 5 |
| 8 |
解答:解:(1)摸出一个球是黄球的概率=
;
(2)画树状图为:

共有12种等可能的结果数,其中两次摸出的球恰好都是红球的占2种,
所以两次摸出的球恰好都是红球的概率=
=
;
(3)根据题意得
=
,
解得n=4.
| 1 |
| 4 |
(2)画树状图为:

共有12种等可能的结果数,其中两次摸出的球恰好都是红球的占2种,
所以两次摸出的球恰好都是红球的概率=
| 2 |
| 12 |
| 1 |
| 6 |
(3)根据题意得
| 1+n |
| n+4 |
| 5 |
| 8 |
解得n=4.
点评:本题考查了列表法与树状图法:利用列表法或树状图法展示所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求解.注意摸出1个球,记下颜色后不放回.

练习册系列答案
相关题目
下列计算正确的是( )
A、
| ||||||||||
B、
| ||||||||||
C、(1+
| ||||||||||
D、
|
若果
=2-a,那么( )
| (a-2)2 |
| A、a<2 | B、a≤2 |
| C、a>2 | D、a≥2 |
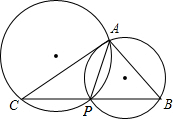 如图,已知,△ABC中,AB=4,AC=3,BC=6,P为BC边上一动点,则△ABP和△ACP的外接圆的半径之比为( )
如图,已知,△ABC中,AB=4,AC=3,BC=6,P为BC边上一动点,则△ABP和△ACP的外接圆的半径之比为( )| A、4﹕3 |
| B、3﹕2 |
| C、2﹕1 |
| D、不确定,与P点的位置有关 |
 在方格纸中建立适当的平面直角坐标系.
在方格纸中建立适当的平面直角坐标系.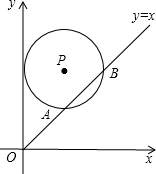 如图,在平面直角坐标系中,⊙P的圆心是(4,a)且(a>2)半径为4,函数y=x的图象被⊙P截得的弦AB的长为
如图,在平面直角坐标系中,⊙P的圆心是(4,a)且(a>2)半径为4,函数y=x的图象被⊙P截得的弦AB的长为