题目内容
在一个袋子里有1个红球9个白球，从中任意摸出1个球后不放回去，再从袋子里摸1个球，那么这次摸到红球的概率是多少？
考点：列表法与树状图法
专题：计算题
分析：先画出树状图展示所有90种等可能的结果数，再找出第二次摸到红球的结果数，然后根据概率公式计算．
解答：解：画树状图为：
，
共有90种等可能的结果数，其中第二次摸到红球的结果数为9，
所以再从袋子里摸1个球，那么这次摸到红球的概率=
=
．
，共有90种等可能的结果数，其中第二次摸到红球的结果数为9，
所以再从袋子里摸1个球，那么这次摸到红球的概率=
| 9 |
| 90 |
| 1 |
| 10 |
点评：本题考查了列表法与树状图法：利用列表法或树状图法展示所有可能的结果求出n，再从中选出符合事件A或B的结果数目m，然后根据概率公式求解．注意从中任意摸出1个球后不放回．
练习册系列答案
相关题目
在方格纸中建立适当的平面直角坐标系．
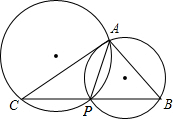如图，已知，△ABC中，AB=4，AC=3，BC=6，P为BC边上一动点，则△ABP和△ACP的外接圆的半径之比为（ ）| A、4﹕3 |
| B、3﹕2 |
| C、2﹕1 |
| D、不确定，与P点的位置有关 |
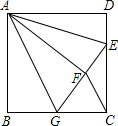如图，正方形ABCD中，AB=6，点E在边CD上，且CD=3DE．将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连接AG、CF．下列结论：①BG=GC：②△ABG≌△AFG；③S△FGC=3；④AG∥CF．其中正确结论是
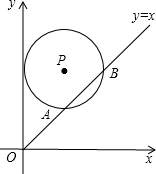如图，在平面直角坐标系中，⊙P的圆心是（4，a）且（a＞2）半径为4，函数y=x的图象被⊙P截得的弦AB的长为下列事件是必然事件的是（ ）
| A、抛掷一枚硬币100次，有50次正面朝上 |
| B、面积相等的两个三角形全等 |
| C、a是实数，则|a|＞0 |
| D、方程x2-2x-100=0必有实数根 |
下列四组数中，其中都不是负数的是（ ）
A、
| ||
B、-56，+3.1，
| ||
| C、-12，-7.5，0 | ||
| D、1，2，-0.23% |