题目内容
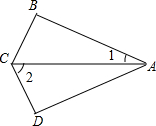如图，将Rt△ABC沿直线AC翻折得到△ADC，其中∠B=90°，∠1=40°，则∠2=（ ）| A、40° | B、50° |
| C、45° | D、60° |
考点：翻折变换（折叠问题）
专题：
分析：先根据图形翻折变换的性质得出∠1=∠DAC，∠ACB=∠2，再由直角三角形的性质即可得出结论．
解答：解：∵将Rt△ABC沿直线AC翻折得到△ADC，∠B=90°，∠1=40°，
∴∠1=∠DAC=40°，∠ACB=∠2，∠D=∠D=90°，
∴∠2=90°-40°=50°．
故选B．
∴∠1=∠DAC=40°，∠ACB=∠2，∠D=∠D=90°，
∴∠2=90°-40°=50°．
故选B．
点评：本题考查的是翻折变换，熟知图形翻折不变性的性质是解答此题的关键．
练习册系列答案
相关题目
若果
=2-a，那么（ ）
| (a-2)2 |
| A、a＜2 | B、a≤2 |
| C、a＞2 | D、a≥2 |
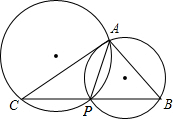如图，已知，△ABC中，AB=4，AC=3，BC=6，P为BC边上一动点，则△ABP和△ACP的外接圆的半径之比为（ ）| A、4﹕3 |
| B、3﹕2 |
| C、2﹕1 |
| D、不确定，与P点的位置有关 |
如图，将矩形ABCD的顶点A翻折，使得A落于边CD上的E处，若AB=5cm，BC=3cm，则折痕BF=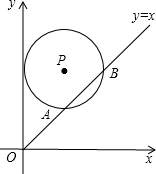
如图，在平面直角坐标系中，⊙P的圆心是（4，a）且（a＞2）半径为4，函数y=x的图象被⊙P截得的弦AB的长为