题目内容
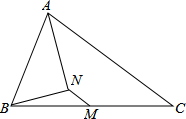 已知在△ABC中,M是BC的中点,AN平分∠BAC,AN⊥BN,求证:MN∥AC.
已知在△ABC中,M是BC的中点,AN平分∠BAC,AN⊥BN,求证:MN∥AC.考点:三角形中位线定理,等腰三角形的判定与性质
专题:证明题
分析:延长BN交AC于D,易得△ABN≌△ADN,则其对应边相等:BN=DN,点N是BD的中点,MN是△BCD的CD边对的中位线,故有MN∥AC.
解答: 证明:延长BN交AC于D,
证明:延长BN交AC于D,
∵AN⊥BN,AN平分∠BAC
∴∠ANB=∠AND,∠BAN=∠DAN.
在△ABN与△ADN中,
,
∴△ABN≌△ADN(SAS),
∴BN=DN,
∴点N是BD的中点
∵点M是BC的中点
∴MN是△BCD的中位线
∴MN∥CD,则MN∥AC.
 证明:延长BN交AC于D,
证明:延长BN交AC于D,∵AN⊥BN,AN平分∠BAC
∴∠ANB=∠AND,∠BAN=∠DAN.
在△ABN与△ADN中,
|
∴△ABN≌△ADN(SAS),
∴BN=DN,
∴点N是BD的中点
∵点M是BC的中点
∴MN是△BCD的中位线
∴MN∥CD,则MN∥AC.
点评:本题考查了全等三角形的判定和性质,三角形中位线定理.作出辅助线ND即可:(1)构造出全等三角形(△ABN≌△ADN),从而求出CE的长;(2)证明MN是中位线,从而轻松解决问题.

练习册系列答案
相关题目
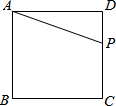 如图,正方形ABCD的边长为4,点P为CD上任意一点(不与C、D重合),设DP=x,四边形ABCP的面积为y.
如图,正方形ABCD的边长为4,点P为CD上任意一点(不与C、D重合),设DP=x,四边形ABCP的面积为y.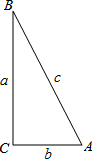 在如图的直角三角形中,我们知道sinα=
在如图的直角三角形中,我们知道sinα=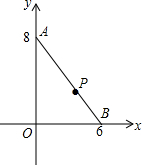 Rt△AOB在平面直角坐标系内的位置如图所示,点O为原点,点A(0,8),点B(6,0),点P在线段AB上,且AP=6.在x轴上存在点Q,使得以B、P、Q为顶点的三角形与△AOB相似.请写出点Q的坐标
Rt△AOB在平面直角坐标系内的位置如图所示,点O为原点,点A(0,8),点B(6,0),点P在线段AB上,且AP=6.在x轴上存在点Q,使得以B、P、Q为顶点的三角形与△AOB相似.请写出点Q的坐标