题目内容
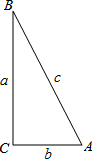 在如图的直角三角形中,我们知道sinα=
在如图的直角三角形中,我们知道sinα=| a |
| c |
| b |
| c |
| a |
| b |
| a2 |
| c2 |
| b2 |
| c2 |
| a2+b2 |
| c2 |
| c2 |
| c2 |
(1)请你根据上面的探索过程,探究sinα,cosα与tanα之间的关系;
(2)请你利用上面探究的结论解答下面问题:已知α为锐角,且tanα=
| 1 |
| 2 |
| sinα-2cosα |
| 2sinα+cosα |
考点:同角三角函数的关系
专题:阅读型
分析:(1)利用sinα=
,cosα=
,tanα=
,即可得出sinα,cosα与tanα之间的关系;
(2)利用(1)中所求得出2sinα=cosα,进而代入原式求出即可.
| a |
| c |
| b |
| c |
| a |
| b |
(2)利用(1)中所求得出2sinα=cosα,进而代入原式求出即可.
解答:解:(1)∵sinα=
,cosα=
,tanα=
,
∴
=
=
,则tanα=
;
(2)∵tanα=
,
∴
=
,
∴2sinα=cosα,
∴
=
=-
.
| a |
| c |
| b |
| c |
| a |
| b |
∴
| sinα |
| cosα |
| ||
|
| a |
| b |
| sinα |
| cosα |
(2)∵tanα=
| 1 |
| 2 |
∴
| sinα |
| cosα |
| 1 |
| 2 |
∴2sinα=cosα,
∴
| sinα-2cosα |
| 2sinα+cosα |
| sinα-4sinα |
| 2sinα+2sinα |
| 3 |
| 4 |
点评:此题主要考查了同角三角函数关系,得出sinα,cosα与tanα之间的关系是解题关键.

练习册系列答案
相关题目
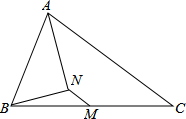 已知在△ABC中,M是BC的中点,AN平分∠BAC,AN⊥BN,求证:MN∥AC.
已知在△ABC中,M是BC的中点,AN平分∠BAC,AN⊥BN,求证:MN∥AC.