题目内容
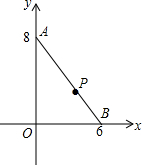 Rt△AOB在平面直角坐标系内的位置如图所示,点O为原点,点A(0,8),点B(6,0),点P在线段AB上,且AP=6.在x轴上存在点Q,使得以B、P、Q为顶点的三角形与△AOB相似.请写出点Q的坐标
Rt△AOB在平面直角坐标系内的位置如图所示,点O为原点,点A(0,8),点B(6,0),点P在线段AB上,且AP=6.在x轴上存在点Q,使得以B、P、Q为顶点的三角形与△AOB相似.请写出点Q的坐标考点:相似三角形的判定,坐标与图形性质
专题:
分析:本题第一问可以直接运用相似性来求得,而第二问则需要分类讨论,这点是容易忽略掉的.
解答: 解:由勾股定理得AB=10,设p点坐标为(x,y),
解:由勾股定理得AB=10,设p点坐标为(x,y),
则由三角形相似可得
=
代入数值可得x=3.6,
=
,
解得y=3.2
故P点坐标为(3.6,3.2).
假设Q点坐标为(q,0),若BP为斜边则q=3.6.
若BQ为斜边,则
=
,解得BQ=
,
因为OB=6,
所以q=-
,
故Q点坐标为(3.6,0)或(-
,0),
故答案为:(3.6,0)或(-
,0).
 解:由勾股定理得AB=10,设p点坐标为(x,y),
解:由勾股定理得AB=10,设p点坐标为(x,y),则由三角形相似可得
| AP |
| AB |
| x |
| OB |
| AB-AP |
| AB |
| y |
| OA |
解得y=3.2
故P点坐标为(3.6,3.2).
假设Q点坐标为(q,0),若BP为斜边则q=3.6.
若BQ为斜边,则
| BP |
| OB |
| BQ |
| AB |
| 20 |
| 3 |
因为OB=6,
所以q=-
| 2 |
| 3 |
故Q点坐标为(3.6,0)或(-
| 2 |
| 3 |
故答案为:(3.6,0)或(-
| 2 |
| 3 |
点评:本题需要用到勾股定理以及三角形相似等方面的知识点,在求坐标的时候用方程思想可以更方便些.问题一可直接运用三角形相似求出结果,问题二则需要分情况讨论,Q点坐标不止一个.

练习册系列答案
相关题目
下列说法正确的个数为( )
(1)过两点有且只有一条直线
(2)连接两点的线段叫做两点间的距离
(3)两点之间的所有连线中,线段最短
(4)射线比直线短一半
(5)直线AB和直线BA表示同一条直线.
(1)过两点有且只有一条直线
(2)连接两点的线段叫做两点间的距离
(3)两点之间的所有连线中,线段最短
(4)射线比直线短一半
(5)直线AB和直线BA表示同一条直线.
| A、2 | B、3 | C、4 | D、5 |
 在△ABC中,∠ACB=90°,CD⊥AB交于点D,则下列等式中错误的是( )
在△ABC中,∠ACB=90°,CD⊥AB交于点D,则下列等式中错误的是( )A、sinB=
| ||
B、sinB=
| ||
C、sinB=
| ||
D、sinB=
|
化简:(
)2+
的结果是( )
| 2-x |
| (x-3)2 |
| A、5-2x | B、5 |
| C、2x-5 | D、-2x-1 |
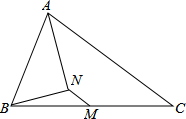 已知在△ABC中,M是BC的中点,AN平分∠BAC,AN⊥BN,求证:MN∥AC.
已知在△ABC中,M是BC的中点,AN平分∠BAC,AN⊥BN,求证:MN∥AC. 如图,AE=CF,∠AFD=∠CEB,DF=BE;△AFD与△CEB全等吗?为什么?
如图,AE=CF,∠AFD=∠CEB,DF=BE;△AFD与△CEB全等吗?为什么?