题目内容
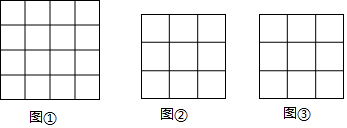
13.正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点,以格点为顶点画图形.(1)在图①中,画一个面积为8的正方形;
(2)在图②,画一个直角三角形,使它们的三边长都是无理数.
(3)图③中,画一个三角形,使它是轴对称图形,并且面积最大.
分析 (1)首先确定边长为2$\sqrt{2}$,再画出图形即可.
(2)根据勾股定理,以及直角三角形的定义即可画出.
(3)根据题意满足条件的三角形为等腰三角形,由此画出面积最大的三角形即可.
解答 解:(1)如图1中,正方形即为所求.
(2)如图2中,直角三角形即为所求.
(3)如图3中,三角形即为所求.
点评 本题考查的是勾股定理、直角三角形的判定、正方形的判定,轴对称图形等知识,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键,需要灵活运用这些知识解决问题,综合性比较强,属于中考常考题型.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
4.化简$\sqrt{4}$的结果是( )
| A. | 2 | B. | ±2 | C. | $\sqrt{2}$ | D. | ±$\sqrt{2}$ |
3.下列“QQ表情”中属于轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |

 如图,点A、B、C、D、E在圆上,弦的延长线与弦的延长线相交于点,AB是圆的直径,D是BC的中点.求证:AB=AC.
如图,点A、B、C、D、E在圆上,弦的延长线与弦的延长线相交于点,AB是圆的直径,D是BC的中点.求证:AB=AC.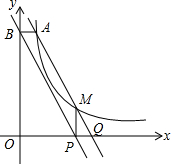 如图,点A(3,2)和点M(m,n)都在反比例函数y=$\frac{k}{x}$(x>0)的图象上.
如图,点A(3,2)和点M(m,n)都在反比例函数y=$\frac{k}{x}$(x>0)的图象上.