��Ŀ����
��ͼ����֪�����ߣ�����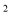 ���������
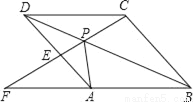
���������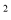 ��4�ᣭ4������ཻ�ڵ�A�͵�B��������ཻ�ڵ�D��0��8����ֱ��DCƽ���ڣ��ᣬ������������һ��C������P��ÿ��2����λ���ȵ��ٶȴ�C���������C��D�˶���ͬʱ����Q��ÿ��1����λ���ȵ��ٶȴӵ�A��������A��B�˶�������PQ��CB�����P�˶���ʱ��Ϊt�룮
��4�ᣭ4������ཻ�ڵ�A�͵�B��������ཻ�ڵ�D��0��8����ֱ��DCƽ���ڣ��ᣬ������������һ��C������P��ÿ��2����λ���ȵ��ٶȴ�C���������C��D�˶���ͬʱ����Q��ÿ��1����λ���ȵ��ٶȴӵ�A��������A��B�˶�������PQ��CB�����P�˶���ʱ��Ϊt�룮
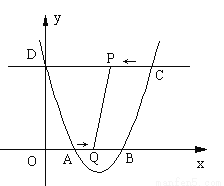
����������ֵ�����������ı���ODPQΪ����ʱ����������ε���������������ı���PQBC���������14ʱ����t��ֵ����������tΪ��ֵʱ����PBQ�ǵ��������Σ���ֱ��д���𰸣�
������8������������������ ���������������� �������������ߣ�������������ᣭ4�ᣭ4�����㣨0��8�� ��ᣭ4�ᣭ4��8 ��ã��6�����2���������⣬��ȥ�� ����ֵΪ6 �������ɣ������ɵ������ߵĽ���ʽΪ ��������6����8 ������0ʱ������6����8��0 ��ã�����2������4 ��A������Ϊ��2��0����B������Ϊ��4��0�� ������...
��ϰ��ϵ�д�
�����Ŀ
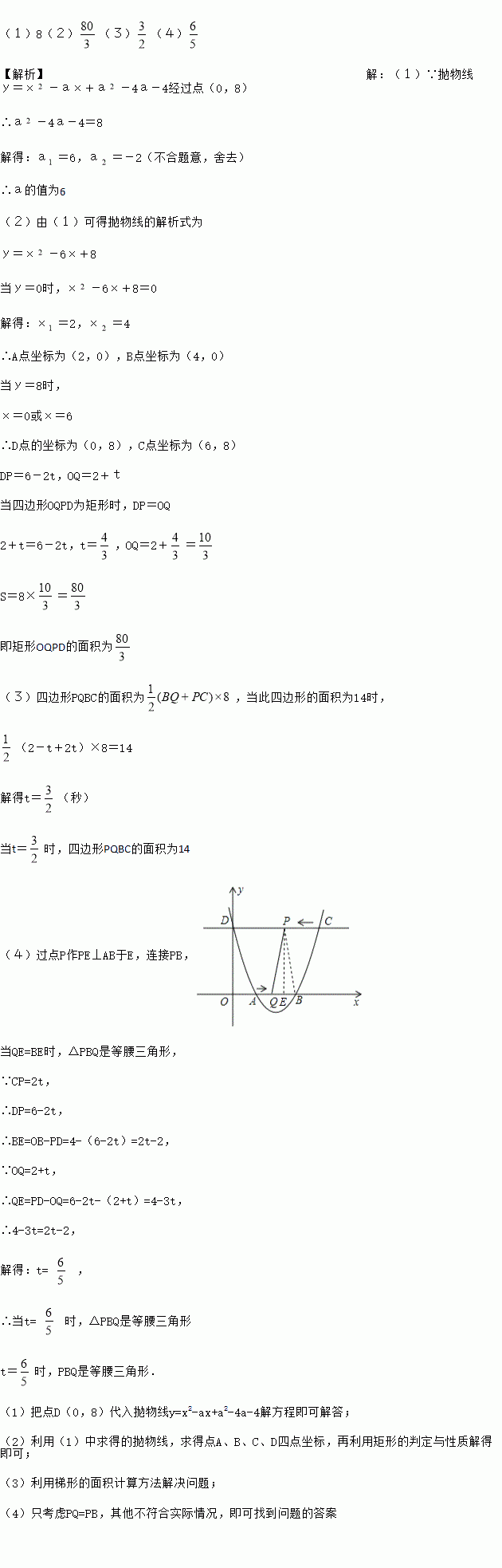

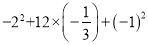
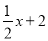 B.
B. 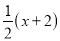 �� C.
�� C. 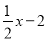 D.
D. 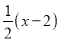
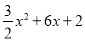 �Ķ���ΪM����y���ཻ�ڵ�N���Ƚ�������C1��x�ᷭ�ۣ�������ƽ��p����λ���Ⱥ�õ�������C2��ֱ��l��y=kx+b����M��N���㣮
�Ķ���ΪM����y���ཻ�ڵ�N���Ƚ�������C1��x�ᷭ�ۣ�������ƽ��p����λ���Ⱥ�õ�������C2��ֱ��l��y=kx+b����M��N���㣮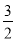 x2+6x+2��kx+b�Ľ⼯��
x2+6x+2��kx+b�Ľ⼯��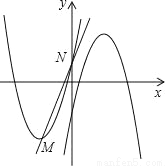
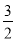 x2+6x��2��3����q=
x2+6x��2��3����q= ʱ��3��4qȡ���ֵ�����ֵΪ��7
ʱ��3��4qȡ���ֵ�����ֵΪ��7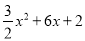 ��x=0����y=2��
��x=0����y=2��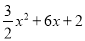 =
=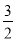 ��x+2��2��4�� ��M����2����4����
��x+2��2��4�� ��M����2����4����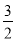 x2+6x+2��kx+b�Ľ⼯Ϊ��2��x��0��
x2+6x+2��kx+b�Ľ⼯Ϊ��2��x��0�� 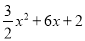 �Ķ���ΪM����2����4����
�Ķ���ΪM����2����4����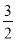 ��x��2��2+4=��
��x��2��2+4=��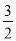 x2+6x��2��
x2+6x��2�� 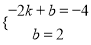 ����ã�
����ã� 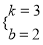 ��
��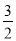 x2+6x��2=3x+2��q��ʵ��������3x2��6x+8��2q��ʵ������
x2+6x��2=3x+2��q��ʵ��������3x2��6x+8��2q��ʵ������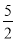 �� �ߩ�4��0��
�� �ߩ�4��0��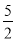 ʱ��3��4qȡ���ֵ�����ֵΪ��7��
ʱ��3��4qȡ���ֵ�����ֵΪ��7��
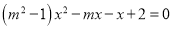 �ǹ���x��һԪһ�η��̣������ʽ|m��1|��ֵΪ����
�ǹ���x��һԪһ�η��̣������ʽ|m��1|��ֵΪ����