题目内容
10.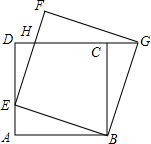 已知,如图,正方形ABCD的边长为1,点E是AD边上的动点,从点A沿AD向D运动,以BE为边,在BE的上方作正方形BEFG,连接CG,请探究:
已知,如图,正方形ABCD的边长为1,点E是AD边上的动点,从点A沿AD向D运动,以BE为边,在BE的上方作正方形BEFG,连接CG,请探究:(1)线段AE与CG是否相等,请说明理由;
(2)求证:△ABE∽△DEH;
(3)当点E在何处时,DH的长度最大,最大长度是多少?
分析 (1)由正方形的性质和互余得到,判断全等三角形;
(2)由正方形的性质和互余得到三角形相似;
(3)由△ABE∽△DEH得到比例式,计算即可.
解答 (1)解:AE=CG,
理由如下:
∵四边形ABCD,BEFG都为正方形,
∴AB=BC,BE=BG,∠ABE=∠CBG,
在△ABE和△CBG中
$\left\{\begin{array}{l}{AB=BC}\\{∠ABE=∠CBG}\\{BE=BG}\end{array}\right.$
∴△ABE≌△CBG,
∴AE=CG
(2)证明:∵四边形ABCD,EFGB都为正方形,
∴∠AEB+DEF=90°
∵∠DEF+DHE=90°,
∴∠AEB=DHE,
∵∠A=∠D
∴△ABE∽△DEH
(3)设DH=y,AE=x,则DE=1-x,
∵△ABE∽△DEH,
∴$\frac{DH}{AE}=\frac{DE}{AB}$,
∴$\frac{y}{x}=\frac{1-x}{1}$,
∴y=-x2+x=-(x-$\frac{1}{2}$)2+$\frac{1}{4}$,
∴当x=$\frac{1}{2}$时,ymax=$\frac{1}{4}$,
∴当点E在AD的中点时,DH的最大值为$\frac{1}{4}$.
点评 此题是相似的综合题,主要考查正方形的性质和三角形全等和相似,解本题的关键是有全等和相似得到线段的关系.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
18.小华上周每天的睡眠时间为(单位:小时):7,8,10,11,8,8,9.这组数据的众数是( )
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
19.若分式$\frac{|x|-2}{{x}^{2}-4x+4}$的值为0,则x的值为( )
| A. | 2 | B. | -2 | C. | 2或-2 | D. | 2或3 |
 如图,∠1=∠2,∠3+∠4=180°,问a与c的关系如何?为什么?
如图,∠1=∠2,∠3+∠4=180°,问a与c的关系如何?为什么?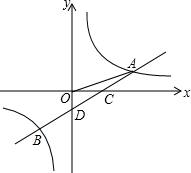 如图,一次函数y=ax+b的图象与反比例函数$y=\frac{k}{x}$的图象交于A,B两点,与x轴交于点C,与y轴交于点D,AE垂直x轴于E点,已知$OA=\sqrt{10}$,OE=3AE,点B的坐标为(m,-2).
如图,一次函数y=ax+b的图象与反比例函数$y=\frac{k}{x}$的图象交于A,B两点,与x轴交于点C,与y轴交于点D,AE垂直x轴于E点,已知$OA=\sqrt{10}$,OE=3AE,点B的坐标为(m,-2). 在图中建立适当的直角坐标系表示图中各景点位置.
在图中建立适当的直角坐标系表示图中各景点位置.