题目内容
2.计算:(1)(-x)•x2•(-x)6
(2)(p-q)4÷(q-p)3•(p-q)2
(3)(-$\frac{1}{4}$)-1+(-2)2×50-($\frac{1}{2}$)-2
(4)(y4)2+(y2)3•y2.
分析 (1)先根据幂的乘方与积的乘方法则计算出(-x)6 的值,再根据单项式乘单项式的性质计算.
(2)先把底数都化为(p-q),然后根据同底数幂的除法法则求解.
(3)先算乘方,再算乘法,再算加法.
(4)先算乘方,然后根据同底数幂的乘法法则运算,最后算加法.
解答 解:(1)(-x)•x2•(-x)6
=-x•x2•x6
=-x9;
(2)(p-q)4÷(q-p)3•(p-q)2;
=-(p-q)•(p-q)2
=-(p-q)3;
(3)(-$\frac{1}{4}$)-1+(-2)2×50-($\frac{1}{2}$)-2
=-4+4×1-4
=-4;
(4)(y4)2+(y2)3•y2
=y8+y6•y2
=y8+y8
=2y8.
点评 此题主要考查了整式的混合运算,正确掌握运算法则是解题关键.

练习册系列答案
相关题目
7.若方程组$\left\{\begin{array}{l}3x+5y=a+4\\ x+3y=2a\end{array}\right.$的解x与y的值的和为3,则a的值为( )
| A. | -3 | B. | -2 | C. | 2 | D. | 10 |
14.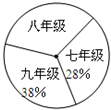 阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.1995年联合国教科文组织把每年4月23日确定为“世界读书日”.表1是某校初中三个年级学生阅读课外书籍情况统计表,图2是该校初中三个年级学生入数分布扇形统计图,其中八年级人数为408人.
阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.1995年联合国教科文组织把每年4月23日确定为“世界读书日”.表1是某校初中三个年级学生阅读课外书籍情况统计表,图2是该校初中三个年级学生入数分布扇形统计图,其中八年级人数为408人.
请你根据图表中的信息,解答下列问题:
(1)表中的a=2400,b=0.35;请补全扇形统计图;
(2)求该校初中学生平均每人读多少本课外书;
(3)在阋读“科普常识”的5名学生中有3男2女,在这5人中,学校打算随杌选2位进行采访,请你用列表法或树状图法求出所选2位恰妤都为男性的概率.
 阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.1995年联合国教科文组织把每年4月23日确定为“世界读书日”.表1是某校初中三个年级学生阅读课外书籍情况统计表,图2是该校初中三个年级学生入数分布扇形统计图,其中八年级人数为408人.
阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.1995年联合国教科文组织把每年4月23日确定为“世界读书日”.表1是某校初中三个年级学生阅读课外书籍情况统计表,图2是该校初中三个年级学生入数分布扇形统计图,其中八年级人数为408人.| 图书种类 | 频数 | 频率 |
| 科普常识 | 840 | b |
| 名人传记 | 816 | 0.34 |
| 漫画丛书 | a | 0.25 |
| 表(1) 其它 | 144 | 0.06 |
(1)表中的a=2400,b=0.35;请补全扇形统计图;
(2)求该校初中学生平均每人读多少本课外书;
(3)在阋读“科普常识”的5名学生中有3男2女,在这5人中,学校打算随杌选2位进行采访,请你用列表法或树状图法求出所选2位恰妤都为男性的概率.
11.式子$\sqrt{x+3}$有意义的条件是( )
| A. | x≥3 | B. | x>3 | C. | x≥-3 | D. | x>-3 |
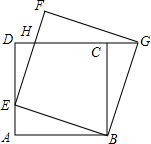 已知,如图,正方形ABCD的边长为1,点E是AD边上的动点,从点A沿AD向D运动,以BE为边,在BE的上方作正方形BEFG,连接CG,请探究:
已知,如图,正方形ABCD的边长为1,点E是AD边上的动点,从点A沿AD向D运动,以BE为边,在BE的上方作正方形BEFG,连接CG,请探究: 如图,四个有理数在数轴上的对应点分别是M、N、P、Q,若点M,Q表示的有理数互为相反数,则图中表示绝对值最小的数的点是N.
如图,四个有理数在数轴上的对应点分别是M、N、P、Q,若点M,Q表示的有理数互为相反数,则图中表示绝对值最小的数的点是N.