题目内容
1.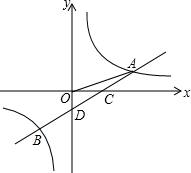 如图,一次函数y=ax+b的图象与反比例函数$y=\frac{k}{x}$的图象交于A,B两点,与x轴交于点C,与y轴交于点D,AE垂直x轴于E点,已知$OA=\sqrt{10}$,OE=3AE,点B的坐标为(m,-2).
如图,一次函数y=ax+b的图象与反比例函数$y=\frac{k}{x}$的图象交于A,B两点,与x轴交于点C,与y轴交于点D,AE垂直x轴于E点,已知$OA=\sqrt{10}$,OE=3AE,点B的坐标为(m,-2).(1)求反比例函数的解析式.
(2)求一次函数的解析式.
(3)在y轴上存在一点P,使得△PDC与△ODC相似,请你求出P点的坐标.
分析 (1)过A作AE垂直x轴,垂足为E,根据OE=3AE,以及OA的长,利用勾股定理求出AE与OE的长,确定出A的坐标,代入双曲线解析式求出k的值,即可确定出反比例解析式;
(2)把B坐标代入反比例解析式求出m的值,确定出B坐标,再由A坐标,利用待定系数法求出一次函数解析式即可;
(3)过点C作CP⊥AB,垂足为点C,求出一次函数与坐标轴的交点确定出C与D坐标,求出DC的长,由△PDC与△ODC相似,得比例,求出PD的长,由PD-OD求出OP的长,即可确定出P坐标.
解答 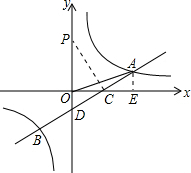 解:(1)过A作AE垂直x轴,垂足为E,
解:(1)过A作AE垂直x轴,垂足为E,
∵OE=3AE,OA=$\sqrt{10}$,
∴在Rt△AOE中,根据勾股定理得:OE2+AE2=10,
∴AE=1,OE=3,
∴点A的坐标为(3,1).
∵A点在双曲线上,
∴1=$\frac{k}{3}$,即k=3,
则双曲线的解析式为y=$\frac{3}{x}$;
(2)∵点B(m,-2)在双曲线y=$\frac{3}{x}$上,
∴-2=$\frac{3}{m}$,
∴m=-$\frac{3}{2}$,
∴点B的坐标为(-$\frac{3}{2}$,-2),
设一次函数解析式为y=ax+b,
把A与B坐标代入得:$\left\{\begin{array}{l}{3a+b=1}\\{-\frac{3}{2}a+b=-2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{2}{3}}\\{b=-1}\end{array}\right.$,
则一次函数的解析式为y=$\frac{2}{3}$x-1;
(3)过点C作CP⊥AB,垂足为点C,
∵C,D两点在直线y=$\frac{2}{3}$x-1上,
∴C,D的坐标分别是:C($\frac{3}{2}$,0),D(0,-1),即OC=$\frac{3}{2}$,OD=1,
∴DC=$\frac{\sqrt{13}}{2}$,
∵△PDC∽△CDO,
∴$\frac{PD}{DC}$=$\frac{DC}{OD}$,
∴PD=$\frac{D{C}^{2}}{OD}$=$\frac{13}{4}$,
又OP=DP-OD=$\frac{13}{4}$-1=$\frac{9}{4}$,
∴P点坐标为(0,$\frac{9}{4}$).
点评 此题属于反比例函数综合题,涉及的知识有:待定系数法确定反比例、一次函数解析式,坐标与图形性质,相似三角形的性质,以及勾股定理,熟练掌握待定系数法是解本题的关键.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案| A. | x≥3 | B. | x>3 | C. | x≥-3 | D. | x>-3 |
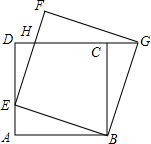 已知,如图,正方形ABCD的边长为1,点E是AD边上的动点,从点A沿AD向D运动,以BE为边,在BE的上方作正方形BEFG,连接CG,请探究:
已知,如图,正方形ABCD的边长为1,点E是AD边上的动点,从点A沿AD向D运动,以BE为边,在BE的上方作正方形BEFG,连接CG,请探究: