题目内容
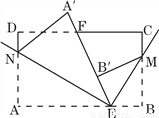
如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF,将∠BEF对折点B落在直线EF上的点B′处,得折痕EM;将∠AEF对折,点A落在直线EF上的点A′处,得折痕EN,求∠NEM的度数,并直接写出∠B′ME互余的角.
练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
题目内容
如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF,将∠BEF对折点B落在直线EF上的点B′处,得折痕EM;将∠AEF对折,点A落在直线EF上的点A′处,得折痕EN,求∠NEM的度数,并直接写出∠B′ME互余的角.

 一课一练课时达标系列答案
一课一练课时达标系列答案