题目内容
 如图,已知点B,C分别在射线AN,AM上,∠MCB与∠NBC的平分线交于点P.
如图,已知点B,C分别在射线AN,AM上,∠MCB与∠NBC的平分线交于点P.(1)求证:AP平分∠BAC;
(2)若∠ACB=90°,PC=4
| 2 |
考点:角平分线的性质
专题:
分析:(1)过点P作PD⊥AM,PF⊥AN,PE⊥BC,垂足分别为D、F、E,根据角平分线的性质得出PD=PE,PF=PE,故PD=PF,由此可得出结论;
(2)根据∠ACB=90°可知∠ECD=90°.由PC平分∠BCD得出∠PCE=∠CPE=45°,故CE=PE=
PC=4,PF=PE=4,再根据勾股定理即可得出结论.
(2)根据∠ACB=90°可知∠ECD=90°.由PC平分∠BCD得出∠PCE=∠CPE=45°,故CE=PE=
| ||
| 2 |
解答: (1)证明:过点P作PD⊥AM,PF⊥AN,PE⊥BC,垂足分别为D、F、E,
(1)证明:过点P作PD⊥AM,PF⊥AN,PE⊥BC,垂足分别为D、F、E,
∵∠MCB与∠NBC的平分线交于点P.
∴PD=PE,PF=PE,
∴PD=PF,
∴AP平分∠BAC;
(2)解:∵∠ACB=90°,
∴∠ECD=90°.
∵PC平分∠BCD,
∴∠PCE=∠CPE=45°,CE=PE=
PC=4.
∴PF=PE=4,BF=
=
=3,
∴AP=
=
=2
.
 (1)证明:过点P作PD⊥AM,PF⊥AN,PE⊥BC,垂足分别为D、F、E,
(1)证明:过点P作PD⊥AM,PF⊥AN,PE⊥BC,垂足分别为D、F、E,∵∠MCB与∠NBC的平分线交于点P.
∴PD=PE,PF=PE,
∴PD=PF,
∴AP平分∠BAC;
(2)解:∵∠ACB=90°,
∴∠ECD=90°.
∵PC平分∠BCD,
∴∠PCE=∠CPE=45°,CE=PE=
| ||
| 2 |
∴PF=PE=4,BF=
| PB2-PF2 |
| 52-42 |
∴AP=
| AF2+PF2 |
| 102+42 |
| 29 |
点评:本题考查的是角平分线的性质,熟知角的平分线上的点到角的两边的距离相等是解答此题的关键.

练习册系列答案
相关题目
 如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=6,点D是边BC的中点,点E是边AB上的任意一点(点E不与点B重合),沿DE翻折△DBE使点B落在点F处,连接AF,则线段AF长的最小值是
如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=6,点D是边BC的中点,点E是边AB上的任意一点(点E不与点B重合),沿DE翻折△DBE使点B落在点F处,连接AF,则线段AF长的最小值是4的算术平方根为( )
| A、2 | B、±2 | C、-2 | D、16 |
 如图,线段AC、BD交于点M,过B、D两点分别作AC的垂线段BF、DE,
如图,线段AC、BD交于点M,过B、D两点分别作AC的垂线段BF、DE, 如图,∠ABD=90°,CE=AD,BE=BD,求证:CF⊥AD.
如图,∠ABD=90°,CE=AD,BE=BD,求证:CF⊥AD.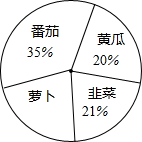 阿姨在一块蔬菜地里种植了4种不同的蔬菜,各种蔬菜的种植面积分布如图.
阿姨在一块蔬菜地里种植了4种不同的蔬菜,各种蔬菜的种植面积分布如图. 如图,在△ABC中,∠C=90°,∠BAC=60°,AC=1,点D在BC上,点E在AB上,使得△ADE是等腰直角三角形,∠ADE=90°,求BE的长.(提示:可以运用“直角三角形中,30°角所对的直角边等于斜边的一半”).
如图,在△ABC中,∠C=90°,∠BAC=60°,AC=1,点D在BC上,点E在AB上,使得△ADE是等腰直角三角形,∠ADE=90°,求BE的长.(提示:可以运用“直角三角形中,30°角所对的直角边等于斜边的一半”).