题目内容
5.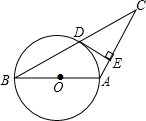 如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过D作DE⊥AC,E为垂足.
如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过D作DE⊥AC,E为垂足.(1)求证:DE是⊙O的切线;
(2)若AB=5,BC=8,求DE+CE的长.
分析 (1)连结OD、AD,先利用圆周角定理得到∠ADB=90°,再利用等腰三角形的性质得BD=CD,于是可判断OD为△ABC的中位线,则OD∥AC,然后证明DE⊥OD,则根据切线的判定定理即可得到结论;
(2)先由(1)得∠ADC=90°,CD=$\frac{1}{2}$BC=4,再在Rt△ADC中利用勾股定理计算出AD,再利用面积法计算出DE,接着利用勾股定理计算出CE,从而可得CE+DE的长.
解答 (1)证明:连结OD、AD,如图,
∵AB为直径,
∴∠ADB=90°,即AD⊥BC,
∵AB=AC,
∴BD=CD,
而OA=OB,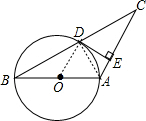
∴OD为△ABC的中位线,
∴OD∥AC,
∵DE⊥AC,
∴DE⊥OD,
∴DE是⊙O的切线;
(2)解:由(1)得∠ADC=90°,CD=$\frac{1}{2}$BC=4,
而AC=AB=5,
在Rt△ADC中,AD=$\sqrt{{5}^{2}-{4}^{2}}$=3,
∵$\frac{1}{2}$DE•AC=$\frac{1}{2}$•AD•CD,
∴DE=$\frac{3×4}{5}$=$\frac{12}{5}$,
在Rt△CDE中,CE=$\sqrt{{4}^{2}-(\frac{12}{5})^{2}}$=$\frac{16}{5}$,
∴DE+CE=$\frac{12}{5}$+$\frac{16}{5}$=$\frac{28}{5}$.
点评 本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.解决(1)小题的关键是证明OD∥AC.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
15.某楼盘商品房成交价今年3月份为a元/m3,4月份比3月份减少了8%,若4月份到6月份平均增长率为12%,则6月份商品房成交价是( )
| A. | a(1-8%)(1+12%)元 | B. | a(1-8%)(1+12%)2元 | C. | (a-8%)(a+12%)元 | D. | a(1-8%+12%)元 |
 如图,AD∥BC,∠B=30°,DB平分∠ADE,则∠ADE的度数为60°.
如图,AD∥BC,∠B=30°,DB平分∠ADE,则∠ADE的度数为60°.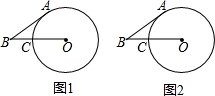 BA与⊙O相切,切点为A,连接OB交⊙O于点C.
BA与⊙O相切,切点为A,连接OB交⊙O于点C.