题目内容
10.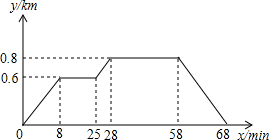 已知小明家、食堂、图书馆在同一直线上.小明从家去食堂吃早餐,接着去图书馆读报,然后回家.如图反映了这个过程中,小明离家的距离y与时间x之间的对应关系,根据图象可得,当25≤x≤28时,y与x的函数关系式是y=$\frac{1}{15}$x-$\frac{16}{15}$.
已知小明家、食堂、图书馆在同一直线上.小明从家去食堂吃早餐,接着去图书馆读报,然后回家.如图反映了这个过程中,小明离家的距离y与时间x之间的对应关系,根据图象可得,当25≤x≤28时,y与x的函数关系式是y=$\frac{1}{15}$x-$\frac{16}{15}$.
分析 根据当25≤x≤28时,函数经过(25,0.6),(28,0.8),由待定系数法可求y与x的函数关系式.
解答 解:∵当25≤x≤28时,函数经过(25,0.6),(28,0.8),
∴设y与x的函数关系式是y=kx+b,则$\left\{\begin{array}{l}{25k+b=0.6}\\{28k+b=0.8}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{1}{15}}\\{b=-\frac{16}{15}}\end{array}\right.$.
故y与x的函数关系式是y=$\frac{1}{15}$x-$\frac{16}{15}$.
故答案为:y=$\frac{1}{15}$x-$\frac{16}{15}$.
点评 本题考查了一次函数的应用,观察图象和熟练掌握待定系数法是解题关键.

练习册系列答案
相关题目
19.以下列各组数为长度的线段,能构成直角三角形的是( )
| A. | 2,3,4 | B. | 2.5,4,5.5 | C. | 5,12,13 | D. | 8,15,16 |
18. 甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.当甲、乙两车相距50千米时,时间t的值最多有( )
甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.当甲、乙两车相距50千米时,时间t的值最多有( )
 甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.当甲、乙两车相距50千米时,时间t的值最多有( )
甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.当甲、乙两车相距50千米时,时间t的值最多有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
15.(-3)2=( )
| A. | -6 | B. | -1 | C. | -9 | D. | 9 |
19.若(x-1)2+$\sqrt{y+2}$=0,则x+y的值是( )
| A. | -3 | B. | -1 | C. | 1 | D. | 3 |
20. 为了了解某车间工人日加工零件数的情况,车间负责人通过统计数据绘制成如图所示的条形统计图,则下列说法正确的是( )
为了了解某车间工人日加工零件数的情况,车间负责人通过统计数据绘制成如图所示的条形统计图,则下列说法正确的是( )
 为了了解某车间工人日加工零件数的情况,车间负责人通过统计数据绘制成如图所示的条形统计图,则下列说法正确的是( )
为了了解某车间工人日加工零件数的情况,车间负责人通过统计数据绘制成如图所示的条形统计图,则下列说法正确的是( )| A. | 这些工人日加工零件数的众数是10个,中位数是7个 | |
| B. | 这些工人日加工零件数的众数是6个,中位数是6个 | |
| C. | 这些工人日加工零件数的众数是10个,中位数是5.5个 | |
| D. | 这些工人日加工零件数的众数是6个,中位数是5.5个 |
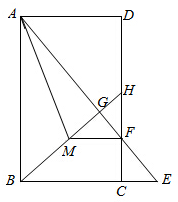 如图所示,在矩形ABCD中,点E是边BC延长线上一点,连结AE,交DC于点F,作BH⊥AE于点G,交DC于点H,作FM∥BC交BH于点M,连结AM.且FH=FE.AD=2$\sqrt{7}$.AG=6.
如图所示,在矩形ABCD中,点E是边BC延长线上一点,连结AE,交DC于点F,作BH⊥AE于点G,交DC于点H,作FM∥BC交BH于点M,连结AM.且FH=FE.AD=2$\sqrt{7}$.AG=6.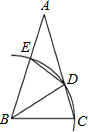 △ABC中,AB=AC,∠A=30°,以B为圆心,BC长为半径画弧,分别交AC,AB于D,E两点,并连结BD,DE. 则∠BDE的度数为67.5°.
△ABC中,AB=AC,∠A=30°,以B为圆心,BC长为半径画弧,分别交AC,AB于D,E两点,并连结BD,DE. 则∠BDE的度数为67.5°.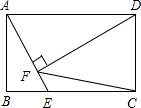 如图,在矩形ABCD中,AB=2$\sqrt{2}$,AD=4,点E是BC边上一个动点,连接AE,作DF⊥AE于点F,当BE的长为2或2$\sqrt{2}$或4-2$\sqrt{2}$时,△CDF是等腰三角形.
如图,在矩形ABCD中,AB=2$\sqrt{2}$,AD=4,点E是BC边上一个动点,连接AE,作DF⊥AE于点F,当BE的长为2或2$\sqrt{2}$或4-2$\sqrt{2}$时,△CDF是等腰三角形.