题目内容
11.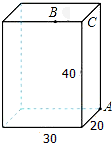 如图所示,长方体的长为30cm,宽为20cm,高为40cm,点B离点C的距离为10cm.已知蚂蚁如果要沿着长方体的表面从点A爬到点B,则需要爬行的最短路程是50cm.
如图所示,长方体的长为30cm,宽为20cm,高为40cm,点B离点C的距离为10cm.已知蚂蚁如果要沿着长方体的表面从点A爬到点B,则需要爬行的最短路程是50cm.
分析 画出长方体的侧面展开图,根据勾股定理求出AB的长即可、
解答 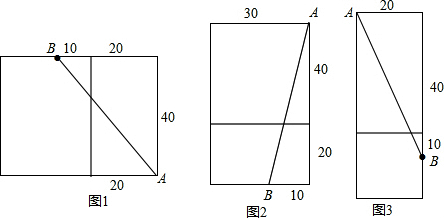 解:如图1所示,
解:如图1所示,
AB=$\sqrt{{40}^{2}+(10+20)^{2}}$=$\sqrt{2500}$=50cm.
如图2所示,
AB=$\sqrt{{10}^{2}+{(40+20)}^{2}}$=$\sqrt{3700}$=10$\sqrt{37}$cm;
如图3所示,
AB=$\sqrt{{20}^{2}+{(40+10)}^{2}}$=$\sqrt{2900}$=10$\sqrt{29}$cm,
∵$\sqrt{2500}$<$\sqrt{2900}$<$\sqrt{3700}$,
∴爬行的最短路程是50cm.
故答案为:50.
点评 本题考查的是平面展开-最短路径问题,根据题意画出长方体的侧面展开图,根据勾股定理求解是解答此题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
2.从2开始,连续的偶数相加,它们的和的情况如下表:当n个由2开始的连续偶数相加时,它们的和S与n之间有什么样的关系?用n的式子表示出来,并由此计算.
(1)若n=8时,则S的值为72;
(2)根据表中的规律猜想:用n的式子表示S的公式为:S=2+4+6+6…+2n=n(n+1);
(3)根据(2)题的公式,计算:102+104+106+…+2012+2014.
| 加数的个数(n) | 和(S) |
| 1 | 2=1×2 |
| 2 | 2+4=2×3 |
| 3 | 2+4+6=12=3×4 |
| 4 | 2+4+6+8=20=4×5 |
| 5 | 2+6+6+8+10=30=5×6 |
| … | … |
(2)根据表中的规律猜想:用n的式子表示S的公式为:S=2+4+6+6…+2n=n(n+1);
(3)根据(2)题的公式,计算:102+104+106+…+2012+2014.
19.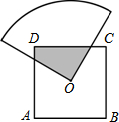 如图,O是边长为a的正方形ABCD的中心,将一块半径足够长,圆心为直角的扇形纸板的圆心放在O点处,并将纸板的圆心绕O旋转,求正方形ABCD的边被纸板覆盖部分的面积为( )
如图,O是边长为a的正方形ABCD的中心,将一块半径足够长,圆心为直角的扇形纸板的圆心放在O点处,并将纸板的圆心绕O旋转,求正方形ABCD的边被纸板覆盖部分的面积为( )
 如图,O是边长为a的正方形ABCD的中心,将一块半径足够长,圆心为直角的扇形纸板的圆心放在O点处,并将纸板的圆心绕O旋转,求正方形ABCD的边被纸板覆盖部分的面积为( )
如图,O是边长为a的正方形ABCD的中心,将一块半径足够长,圆心为直角的扇形纸板的圆心放在O点处,并将纸板的圆心绕O旋转,求正方形ABCD的边被纸板覆盖部分的面积为( )| A. | $\frac{1}{2}{a^2}$ | B. | $\frac{1}{3}{a^2}$ | C. | $\frac{1}{4}{a^2}$ | D. | 无法计算 |
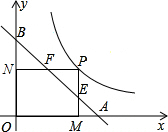 如图,双曲线y=$\frac{1}{2x}$(x>0)上有一动点P,作PM⊥x轴于M,PN⊥y轴于N,直线AB:y=-x+1分别交PM、PN于点E、F.
如图,双曲线y=$\frac{1}{2x}$(x>0)上有一动点P,作PM⊥x轴于M,PN⊥y轴于N,直线AB:y=-x+1分别交PM、PN于点E、F.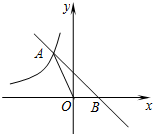 如图,直线y=-x+b与双曲线$y=-\frac{1}{x}$(x<0)交于点A,与x轴交于点B,则OA2-OB2=( )
如图,直线y=-x+b与双曲线$y=-\frac{1}{x}$(x<0)交于点A,与x轴交于点B,则OA2-OB2=( )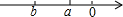 如图,a,b所在数轴的位置,化简下列各式:
如图,a,b所在数轴的位置,化简下列各式: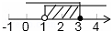
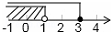
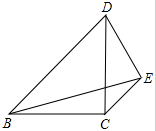 如图,等腰直角△BCD中,BC=CD,E是边CD外的一点,且CE∥BD,BE=BD,则CE:BD的值$\frac{\sqrt{3}-1}{2}$.
如图,等腰直角△BCD中,BC=CD,E是边CD外的一点,且CE∥BD,BE=BD,则CE:BD的值$\frac{\sqrt{3}-1}{2}$.