题目内容
16.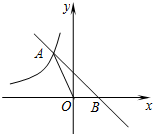 如图,直线y=-x+b与双曲线$y=-\frac{1}{x}$(x<0)交于点A,与x轴交于点B,则OA2-OB2=( )
如图,直线y=-x+b与双曲线$y=-\frac{1}{x}$(x<0)交于点A,与x轴交于点B,则OA2-OB2=( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 由直线y=-x+b与双曲线$y=-\frac{1}{x}$(x<0)交于点A可知:x+y=b,xy=-1,又OA2=x2+y2,OB2=b2,由此即可求出OA2-OB2的值.
解答 解:∵直线y=-x+b与双曲线$y=-\frac{1}{x}$(x<0)交于点A,
设A的坐标(x,y),
∴x+y=b,xy=-1,
而直线y=-x+b与x轴交于B点,
∴OB=b
∴又OA2=x2+y2,OB2=b2,
∴OA2-OB2=x2+y2-b2=(x+y)2-2xy-b2=b2+2-b2=2.
故选B.
点评 本题考查了一次函数与反比例函数的图形和性质,也考查了图象交点坐标和解析式的关系;此题难度较大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.要了解下面的信息,适用普查的是( )
| A. | 深圳所有私家车每天的碳排放总量 | B. | 首届深圳国际马拉松的直播收视率 | ||
| C. | 全国中小学生的近视率 | D. | 校篮球队男队全体队员的平均身高 |
1.直角三角形绕其一直角边旋转一周形成( )
| A. | 圆柱 | B. | 圆锥 | C. | 三棱锥 | D. | 以上都不对 |
5.下列线段能构成直角三角形的是( )
| A. | 3,5,7 | B. | 5,7,8 | C. | 4,6,7 | D. | 5,12,13 |
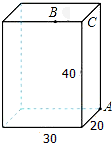 如图所示,长方体的长为30cm,宽为20cm,高为40cm,点B离点C的距离为10cm.已知蚂蚁如果要沿着长方体的表面从点A爬到点B,则需要爬行的最短路程是50cm.
如图所示,长方体的长为30cm,宽为20cm,高为40cm,点B离点C的距离为10cm.已知蚂蚁如果要沿着长方体的表面从点A爬到点B,则需要爬行的最短路程是50cm.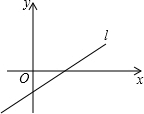 已知直线l:y=(m-3)x+n-2(m,n为常数)的图象如图所示.
已知直线l:y=(m-3)x+n-2(m,n为常数)的图象如图所示.