题目内容
19.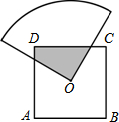 如图,O是边长为a的正方形ABCD的中心,将一块半径足够长,圆心为直角的扇形纸板的圆心放在O点处,并将纸板的圆心绕O旋转,求正方形ABCD的边被纸板覆盖部分的面积为( )
如图,O是边长为a的正方形ABCD的中心,将一块半径足够长,圆心为直角的扇形纸板的圆心放在O点处,并将纸板的圆心绕O旋转,求正方形ABCD的边被纸板覆盖部分的面积为( )| A. | $\frac{1}{2}{a^2}$ | B. | $\frac{1}{3}{a^2}$ | C. | $\frac{1}{4}{a^2}$ | D. | 无法计算 |
分析 如图,作辅助线;由题意可以猜测:阴影部分的面积可能为定值;由旋转变换的性质、正方形的性质可证△ODM≌△OCN,故阴影部分的面积=△COD的面积,即可解决问题.
解答  解:如图,连接OD、OC;
解:如图,连接OD、OC;
∵四边形ABCD为正方形,
∴∠DOC=90°,OD=OC,∠ODM=∠OCN=45°;
∵∠MON=90°,
∴∠MOD=∠NOC;
在△ODM与△OCN中,
$\left\{\begin{array}{l}{∠ODM=∠OCN}\\{OD=OC}\\{∠MOD=∠NOC}\end{array}\right.$,
∴△ODM≌△OCN(ASA),
∴S△MOD=S△NOC,
∴${S}_{阴影}={S}_{△COD}=\frac{1}{4}{a}^{2}$,
故选C.
点评 该题主要考查了旋转变换的性质、正方形的性质、全等三角形的判定及其性质等几何知识点及其应用问题;试题难度中等,为考查分析、解决问题能力的一道好题.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
10.在下列调查中,适宜采用全面调查方式的是( )
| A. | 了解南宁市居民年人均收入 | |
| B. | 了解神州飞船的设备零件的质量情况 | |
| C. | 调查春节联欢晚会的收视率 | |
| D. | 调查五一黄金周期间通行广西高速公路的车流量 |
7.要了解下面的信息,适用普查的是( )
| A. | 深圳所有私家车每天的碳排放总量 | B. | 首届深圳国际马拉松的直播收视率 | ||
| C. | 全国中小学生的近视率 | D. | 校篮球队男队全体队员的平均身高 |
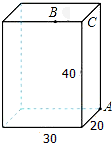 如图所示,长方体的长为30cm,宽为20cm,高为40cm,点B离点C的距离为10cm.已知蚂蚁如果要沿着长方体的表面从点A爬到点B,则需要爬行的最短路程是50cm.
如图所示,长方体的长为30cm,宽为20cm,高为40cm,点B离点C的距离为10cm.已知蚂蚁如果要沿着长方体的表面从点A爬到点B,则需要爬行的最短路程是50cm.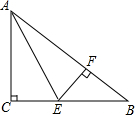 如图,在Rt△ABC中,∠C=90°,∠A的平分线交BC于点E,EF⊥AB于点F,点F恰好是AB的一个三等分点(AF>BF).
如图,在Rt△ABC中,∠C=90°,∠A的平分线交BC于点E,EF⊥AB于点F,点F恰好是AB的一个三等分点(AF>BF).