题目内容
1.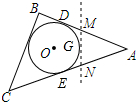 如图,△ABC是一张三角形纸片,⊙O是它的内切圆,点D、E是其中的两个切点,已知AD=6cm,小明准备用剪刀沿着与⊙O相切的一条直线MN剪下一块三角形(△AMN),则剪下的△AMN的周长是12cm.
如图,△ABC是一张三角形纸片,⊙O是它的内切圆,点D、E是其中的两个切点,已知AD=6cm,小明准备用剪刀沿着与⊙O相切的一条直线MN剪下一块三角形(△AMN),则剪下的△AMN的周长是12cm.
分析 根据切线长定理可得AD=AE=6,MD=MG,NG=NE,可以证明△AMN的周长=2AD.
解答 解:如图,设⊙O与直线MN相切于点G,
∵AD、AE是⊙O的切线,
∴AD=AE=6,
又∵MD=MG,NG=NE,
∴△AMN的周长=AM+MN+AN=(AM+MG)+(AN+NG)=(AM+DM)+(AN+NE)=AD+AE=12.
故答案为:12cm
点评 本题考查三角形内切圆与内心、切线长定理等知识,解题的关键是灵活应用切线长定理,学会转化的思想,属于中考常考题型.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
11.九年级数学兴趣小组经过市场调查,得到某种运动服每月的销量与售价的相关信息如表:
已知该运动服的进价为每件60元,设售价为x元.
(1)请用含x的式子表示销售该运动服每件的利润;
(2)设销售该运动服的月销量为y元,求y与x的函数解析式.
| 售价(元/件) | 100 | 110 | 120 | 130 | … |
| 月销量(件) | 200 | 180 | 160 | 140 | … |
(1)请用含x的式子表示销售该运动服每件的利润;
(2)设销售该运动服的月销量为y元,求y与x的函数解析式.
 由若干个相同的小立方体搭成的一个几何体的主视图和俯视图如图所示,俯视图的方格中的字母和数字表示该位置上小立方体的个数,求x,y的值.
由若干个相同的小立方体搭成的一个几何体的主视图和俯视图如图所示,俯视图的方格中的字母和数字表示该位置上小立方体的个数,求x,y的值.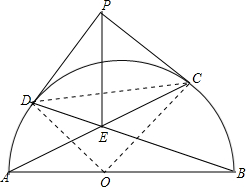 如图所示,AB是半圆O的直径,过点A、B分别作弦AC与BD相交于点E,又过C、D两点引圆的切线交于点P,连结PE,试证:PE⊥AB.
如图所示,AB是半圆O的直径,过点A、B分别作弦AC与BD相交于点E,又过C、D两点引圆的切线交于点P,连结PE,试证:PE⊥AB. 如图,将3枚相同的硬币放入一个3×4的长方形格子中(每个小正方形格子只能放1枚硬币).则所放的3枚硬币中,任意两枚都不同行且不同列的概率为$\frac{6}{55}$.
如图,将3枚相同的硬币放入一个3×4的长方形格子中(每个小正方形格子只能放1枚硬币).则所放的3枚硬币中,任意两枚都不同行且不同列的概率为$\frac{6}{55}$.