题目内容
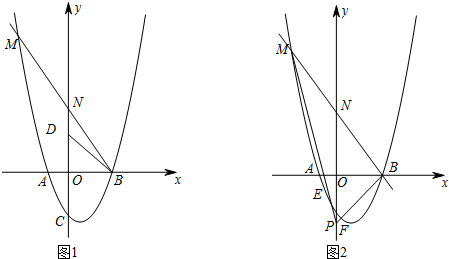
12.已知如图,抛物线y=x2+bx+c经过点A(-1,0)、B(3,0).(1)求b、c的值;
(2)如图,点D与点C关于点O对称,过点B的直线交y轴于点N,交抛物线于另一点M.若∠DBM=∠ACO,求$\frac{MN}{NB}$的值;
(3)如图,在(2)的条件下,点P是y轴上一点,连PM、PB分别交抛物线于点E、F,探究EF与MB的位置关系,并说明理由.
分析 (1)利用待定系数法即可解决问题.
(2)取点Q(1,4),P(0,1),如图1中,作QR⊥y轴于R,连接PQ,则RQ=OP=1,PR=OC=OB=3,由△POR≌△BPO≌△CAO,推出BQ与y轴的交点是N,与抛物线的交点是M,利用方程组即可解决问题.
(3)结论:EF∥BM或EF与BM重合.设P(0,m),求出直线PM、PB,再利用方程组求出点E、F坐标,求出直线EF的解析式即可解决问题.
解答 解:(1)∵抛物线y=x2+bx+c经过点A(-1,0)、B(3,0),
∴有方程组$\left\{\begin{array}{l}{1-b+c=0}\\{9+3b+c=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{b=-2}\\{c=-3}\end{array}\right.$,
∴b=-2,c=-3.
(2)∵抛物线解析式为y=x2-2x-3,
∴点C坐标(0,-3),OA=1,OB=3,OC=3,
∵点D与点C关于点O对称
∴△BOD是等腰直角三角形,∴∠2+∠4=45°,
取点Q(1,4),P(0,1),如图1中,作QR⊥y轴于R,连接PQ,则RQ=OP=1,PR=OC=OB=3,
∴△POR≌△BPO≌△CAO,
∴∠1=∠2=∠α,PQ=PB,
∵∠6+∠2=90°,∴∠1+∠6=90°,
∴∠5=90°,∵PQ=PB,
∴∠3+∠4=45°,∵∠2+∠4=45°,
∴∠DBQ=∠3=∠2=∠α=∠ACO,
∴由此BQ与y轴的交点是N,与抛物线的交点是M,
∵B(3,0),Q(1,4),设直线BQ为y=kx+n,则$\left\{\begin{array}{l}{3k+n=0}\\{k+n=4}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-2}\\{n=6}\end{array}\right.$,
∴直线BN的解析式为y=-2x+6,
∴N(0,6),
由$\left\{\begin{array}{l}{y=-2x+6}\\{y={x}^{2}-2x-3}\end{array}\right.$解得$\left\{\begin{array}{l}{x=-3}\\{y=12}\end{array}\right.$或$\left\{\begin{array}{l}{x=3}\\{y=0}\end{array}\right.$,
∵B(3,0),∴M(-3,12),
作MG⊥y轴于G,
∵N(0,6),M(-3,12),B(3,0),
∴MG=OB=3,NO=NG=6,
∴Rt△MNG≌△Rt△BNO,
∴MN=NB
∴$\frac{MN}{BN}$=1.
(3)结论:EF∥BM或EF与BM重合.
理由:设P(0,m),
∵M(-3,12),B(3,0),
∴可得直线PM的解析式为y=$\frac{m-12}{3}$x+m,直线PB的解析式为y=-$\frac{m}{3}$x+m,
由$\left\{\begin{array}{l}{y=\frac{m-12}{3}x+m}\\{y={x}^{2}-2x-3}\end{array}\right.$消去y得3x2+(6-m)x-3(m+3)=0,
[3x-(m+3)](x+3)=0,
∴x=-3或$\frac{m+3}{3}$,
x=-3时,y=12,
x=$\frac{m+3}{3}$时,y=$\frac{{m}^{2}-36}{9}$,
∴方程组的解为$\left\{\begin{array}{l}{x=-3}\\{y=12}\end{array}\right.$或$\left\{\begin{array}{l}{x=\frac{m+3}{3}}\\{y=\frac{{m}^{2}-36}{9}}\end{array}\right.$,
∴E($\frac{m+3}{3}$,$\frac{{m}^{2}-36}{9}$),
由$\left\{\begin{array}{l}{y=-\frac{m}{3}x+m}\\{y={x}^{2}-2x-3}\end{array}\right.$解得$\left\{\begin{array}{l}{x=3}\\{y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x=-\frac{m+3}{3}}\\{y=\frac{{m}^{2}+12m}{9}}\end{array}\right.$,
∴F(-$\frac{m+3}{3}$,$\frac{{m}^{2}+12m}{9}$),
设直线EF解析式为y=ax+t,
则$\left\{\begin{array}{l}{\frac{{m}^{2}+12m}{9}=-\frac{m+3}{3}a+t}\\{\frac{{m}^{2}-36}{9}=\frac{m+3}{3}a+t}\end{array}\right.$,
∴$\frac{{m}^{2}+12m-{m}^{2}+36}{9}$=-$\frac{2(m+3)}{3}a$,
∴a=-2,
∴直线EF的解析式为y=-2x+t,
∵直线BM的解析式为y=-2x+6,
∴t≠6时,EF∥MB,
t=6时,直线EF与BM重合.
点评 本题考查二次函数综合题、一次函数、待定系数法、全等三角形的判定和性质等知识,解题的关键是熟练掌握这些知识的应用,学会添加辅助线构造全等三角形,学会利用参数解决问题,题目比较难,属于中考压轴题.

 关于这一图案,下列说法正确的是( )
关于这一图案,下列说法正确的是( )| A. | 图案乙是由甲绕BC的中点旋转180°得到的 | |
| B. | 图案乙是由甲绕点C旋转108°得到的 | |
| C. | 图案乙是由甲沿AB方向平移3个边长的距离得到的 | |
| D. | 图案乙是由甲沿直线BC翻转180°得到的 |
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
 如图,已知AB∥DC,AD∥BC,BE=DF,则图中全等的三角形有( )
如图,已知AB∥DC,AD∥BC,BE=DF,则图中全等的三角形有( )| A. | 3对 | B. | 4对 | C. | 5对 | D. | 6对 |
 如图,∠A=∠C=90°,BE,DF分别为∠ABC与∠ADC的平分线,能判断BE∥DF吗?试说明理由.
如图,∠A=∠C=90°,BE,DF分别为∠ABC与∠ADC的平分线,能判断BE∥DF吗?试说明理由.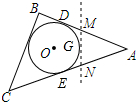 如图,△ABC是一张三角形纸片,⊙O是它的内切圆,点D、E是其中的两个切点,已知AD=6cm,小明准备用剪刀沿着与⊙O相切的一条直线MN剪下一块三角形(△AMN),则剪下的△AMN的周长是12cm.
如图,△ABC是一张三角形纸片,⊙O是它的内切圆,点D、E是其中的两个切点,已知AD=6cm,小明准备用剪刀沿着与⊙O相切的一条直线MN剪下一块三角形(△AMN),则剪下的△AMN的周长是12cm.