题目内容
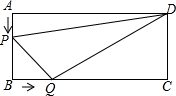 如图,在矩形ABCD中,AB=6cm,BC=12cm,点P点P从A出发沿边AB以1cm/s的速度向点B移动;同时,点Q从点B出发沿边BC以2cm/s的速度向点C移动,(P、Q两点同时停止运动)几秒钟后△PBQ的面积等于28cm2?
如图,在矩形ABCD中,AB=6cm,BC=12cm,点P点P从A出发沿边AB以1cm/s的速度向点B移动;同时,点Q从点B出发沿边BC以2cm/s的速度向点C移动,(P、Q两点同时停止运动)几秒钟后△PBQ的面积等于28cm2?考点:一元二次方程的应用
专题:几何动点问题
分析:设x秒后△PBQ的面积等于28cm2,用含x的代数式分别表示出PB,QB的长,再利用△PBQ的面积等于8列式求值即可;
解答:解:设x秒后△PBQ的面积等于28cm2,由题意列方程
∵AP=x,QB=2x.
∴PB=6-x.
∴
×(6-x)×2x=28,
解得 x1=1,x2=8(舍去).
答:1秒后△PBQ的面积等于28cm2.
∵AP=x,QB=2x.
∴PB=6-x.
∴
| 1 |
| 2 |
解得 x1=1,x2=8(舍去).
答:1秒后△PBQ的面积等于28cm2.
点评:考查一元二次方程的应用;表示出所给三角形的两条直角边长是解决本题的突破点;用到的知识点为:直角三角形的面积=两直角边积的一半.

练习册系列答案
相关题目
直角三角形两条直角边长分别是6和8,则斜边上的中线长为( )
| A、3 | B、4 | C、5 | D、6 |
等腰三角形的两边分别为5和8,那么它的周长是( )
| A、13 | B、18 |
| C、21 | D、18或21 |
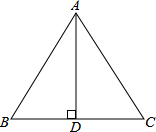 在△ABC中,AB=BC=AC=2cm,AD是BC边上的高,求AD的长和△ABC的面积.
在△ABC中,AB=BC=AC=2cm,AD是BC边上的高,求AD的长和△ABC的面积.