题目内容
如图,若锐角△ABC内接于⊙O,点D在⊙O外(与点C在AB同侧),则下列三个结论:①sin∠C>sin∠D;②cos∠C>cos∠D;③tan∠C>tan∠D中,正确的结论为( )
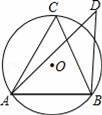

A.①② B.②③ C.①②③ D.①③
D【考点】锐角三角函数的增减性;圆周角定理.
【分析】连接BE,根据圆周角定理,可得∠C=∠AEB,因为∠AEB=∠D+∠DBE,所以∠AEB>∠D,所以∠C>∠D,根据锐角三角形函数的增减性,即可判断.
【解答】解:如图,连接BE,


根据圆周角定理,可得∠C=∠AEB,
∵∠AEB=∠D+∠DBE,
∴∠AEB>∠D,
∴∠C>∠D,
根据锐角三角形函数的增减性,可得,
sin∠C>sin∠D,故①正确;
cos∠C<cos∠D,故②错误;
tan∠C>tan∠D,故③正确;
故选:D.
【点评】本题考查了锐角三角形函数的增减性,解决本题的关键是比较出∠C>∠D.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
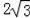
 ,PB= .
,PB= .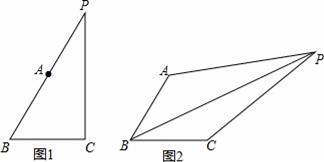

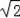
 ≈1.414,
≈1.414,


 的解集是( )
的解集是( ) ,已知在四边形ABCD中,AE、CF分别是∠DAB及∠DCB的平分线,
,已知在四边形ABCD中,AE、CF分别是∠DAB及∠DCB的平分线,
 .
.
