题目内容
9.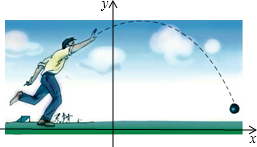 如图,男生张波推铅球,铅球行进高度y(m)与水平距离x(m)之间的关系用如图所示的二次函数图象表示,该二次函数满足y=a(x-4)2+h.他的出手高度为$\frac{5}{3}$m时,铅球推出的距离是10m,
如图,男生张波推铅球,铅球行进高度y(m)与水平距离x(m)之间的关系用如图所示的二次函数图象表示,该二次函数满足y=a(x-4)2+h.他的出手高度为$\frac{5}{3}$m时,铅球推出的距离是10m,(1)求该抛物线的解析式;
(2)若他的出手高度变为2m,铅球推出的距离还是10m时,求铅球行进的最大高度.
分析 (1)把(0,$\frac{5}{3}$),(10,0)代入y=a(x-4)2+h,求出a、h的值即可;
(2)把(0,2),(10,0)代入y=a(x-4)2+h,求出h即可得.
解答 解:(1)把(0,$\frac{5}{3}$),(10,0)代入y=a(x-4)2+h,
得:$\left\{\begin{array}{l}{16a+h=\frac{5}{3}}\\{36a+h=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{1}{12}}\\{h=3}\end{array}\right.$,
∴解析式为y=-$\frac{1}{12}$(x-4)2+3;
(2)把(0,2),(10,0)代入y=a(x-4)2+h,
得:$\left\{\begin{array}{l}{16a+h=2}\\{36a+h=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-0.1}\\{h=3.6}\end{array}\right.$,
∴铅球行进的最大高度为3.6米.
点评 本题主要考查二次函数的实际应用,熟练掌握待定系数法求函数解析式是解题的关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
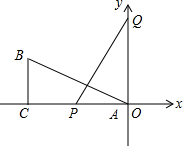 如图,有一个直角△ABC,∠ACB=90°,C(-8,0),B(-8,3),P、Q两点分别在x轴和y轴上运动,且PQ=AB.则当P的坐标为(-8,0),(-3,0)时,才能使△ABC和△PQA全等.
如图,有一个直角△ABC,∠ACB=90°,C(-8,0),B(-8,3),P、Q两点分别在x轴和y轴上运动,且PQ=AB.则当P的坐标为(-8,0),(-3,0)时,才能使△ABC和△PQA全等.