题目内容
20．
如图，在平面直角坐标系中，抛物线y=x2-4x与x轴正半轴交于点A，其顶点为M，将这条抛物线绕点O旋转180°后得到的抛物线与x轴负半轴交于点B，其顶点记为N，连结AM、MB、BN、NA，则四边形AMBN的面积为32．
分析 首先求得抛物线y=x2-4x的顶点M的坐标和与x轴的交点A的坐标，再根据B，N分别关于原点O的对称点是A，M求出B和N点的坐标，求出AB的长，最后根据三角形的面积公式求得结论．
解答 解：∵y=x2-4x=（x-2）2-4，
∴M（2，-4），令y=x2-4x=0，解得：x1=0，x2=4，
∴A（0，4），
∵B，N分别关于原点O的对称点是A，M，
∴B（-4，0），N（-2，4），
∴AB=8，
∴四边形AMBN的面积为：2S△ABM=2×$\frac{1}{2}$×8×4=32，
故答案为：32．
点评 本题主要考查了抛物线与x轴的交点坐标和顶点坐标的求法，中心对称以及三角形面积公式，根据中心对称求得B和N点的坐标是解题的关键．
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
初中暑期衔接系列答案
相关题目
15．
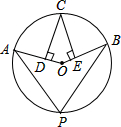如图，点A，B，C，P在⊙O上，CD⊥OA，CE⊥OB，垂足分别为D，E，∠DCE=36°，则∠P的度数为（ ）
如图，点A，B，C，P在⊙O上，CD⊥OA，CE⊥OB，垂足分别为D，E，∠DCE=36°，则∠P的度数为（ ）| A． | 144° | B． | 72° | C． | 60° | D． | 36° |
5．
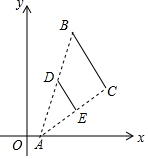如图，线段BC的两端点的坐标分别为B（3，7），C（6，3），以点A（1，0）为位似中心，将线段BC缩小为原来的$\frac{1}{2}$后得到线段DE，则端点D的坐标为（ ）
如图，线段BC的两端点的坐标分别为B（3，7），C（6，3），以点A（1，0）为位似中心，将线段BC缩小为原来的$\frac{1}{2}$后得到线段DE，则端点D的坐标为（ ）| A． | （1，$\frac{7}{2}$） | B． | （2，$\frac{7}{2}$） | C． | （1，2） | D． | （2，2） |
9．
如图，AB∥CD，AE交CD于点C，DE⊥AE于点E，若∠A=42°，则∠D=（ ）
如图，AB∥CD，AE交CD于点C，DE⊥AE于点E，若∠A=42°，则∠D=（ ）| A． | 42° | B． | 58° | C． | 52° | D． | 48° |
