题目内容
 如图,在⊙O中,点P为直径BA延长线上一点,直线PD切⊙O于点D,过点B作BH⊥PD,垂足为H,BH交⊙O于点C,连接BD.
如图,在⊙O中,点P为直径BA延长线上一点,直线PD切⊙O于点D,过点B作BH⊥PD,垂足为H,BH交⊙O于点C,连接BD.(1)求证:BD平分∠ABH;
(2)如果AB=10,BC=6,求BD的长;
(3)在(2)的条件下,当E是
 |
| AB |
考点:切线的性质,勾股定理,相似三角形的判定与性质
专题:
分析:(1)连接OD易证OD∥BH,则∠ODB=∠DBH,然后根据等边对等角证明∠ODB=∠OBD,从而证明;
(2)证明四边形ODHG是矩形,在Rt△DBH中利用勾股定理即可求解;
(3)连接AD,AE,证明△ADE∽△FDB,根据相似三角形的对应边的比相等,即可证得.
(2)证明四边形ODHG是矩形,在Rt△DBH中利用勾股定理即可求解;
(3)连接AD,AE,证明△ADE∽△FDB,根据相似三角形的对应边的比相等,即可证得.
解答: (1)证明:连接OD.
(1)证明:连接OD.
∵PD是⊙O的切线,
∴OD⊥PD.
又∵BH⊥PD,
∴∠PDO=∠PHB=90°,
∴OD∥BH,
∴∠ODB=∠DBH.
∵OD=OB,
∴∠ODB=∠OBD,
∴∠OBD=∠DBH,
∴BD平分∠ABH.
(2)解:过点O作OG⊥BC,G为垂足,
则BG=CG=3,
在Rt△OBG中,OG=
=4.
∵∠ODH=∠DHG=∠HGO=90°,
∴四边形ODHG是矩形.
∴OD=GH=5,DH=OG=4,BH=8.
在Rt△DBH中,BD=4
;
(3)解:连接AD,AE,
则∠AED=∠ABD,∠ADB=90°.
在Rt△ADB中,AD=2
.
又∵E是
的中点,即
=
,∴∠ADE=∠EDB,
∴△ADE∽△FDB.
即
=
,
∴DE•DF=DB•AD=40.
 (1)证明:连接OD.
(1)证明:连接OD. ∵PD是⊙O的切线,
∴OD⊥PD.
又∵BH⊥PD,
∴∠PDO=∠PHB=90°,
∴OD∥BH,
∴∠ODB=∠DBH.
∵OD=OB,
∴∠ODB=∠OBD,
∴∠OBD=∠DBH,
∴BD平分∠ABH.
(2)解:过点O作OG⊥BC,G为垂足,
则BG=CG=3,
在Rt△OBG中,OG=
| OB2-BG2 |
∵∠ODH=∠DHG=∠HGO=90°,
∴四边形ODHG是矩形.
∴OD=GH=5,DH=OG=4,BH=8.
在Rt△DBH中,BD=4
| 5 |
(3)解:连接AD,AE,
则∠AED=∠ABD,∠ADB=90°.
在Rt△ADB中,AD=2
| 5 |
又∵E是
 |
| AB |
 |
| AE |
 |
| BE |
∴△ADE∽△FDB.
即
| DE |
| DB |
| AD |
| FD |
∴DE•DF=DB•AD=40.
点评:本题综合考查了切线的性质,相似三角形的判定与性质,解直角三角形等知识点的运用.此题是一个大综合题,难度较大.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案
相关题目
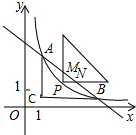 如图,已知反比例函数y=
如图,已知反比例函数y= 如图,在△ABC中,AB=AC,以AB边为直径作⊙O,交BC边于点D,过点D作,DF⊥AC于点F
如图,在△ABC中,AB=AC,以AB边为直径作⊙O,交BC边于点D,过点D作,DF⊥AC于点F