题目内容
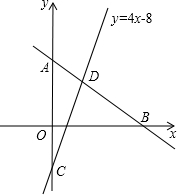 如图,已知直线l与y轴、x轴交于点A(0,8)、B(6,0)两点,直线y=4x-8与y轴、直线l分别交于点C、D,求△ACD绕y轴旋转一周所围成几何体的表面积.
如图,已知直线l与y轴、x轴交于点A(0,8)、B(6,0)两点,直线y=4x-8与y轴、直线l分别交于点C、D,求△ACD绕y轴旋转一周所围成几何体的表面积.考点:两条直线相交或平行问题,点、线、面、体
专题:
分析:根据待定系数法,可求出直线AB,根据两直线的解析式,可得交点坐标,根据勾股定理,可得AD、CD的长,根据旋转一周,可得同底的两个圆锥,根据圆锥的侧面记公式,可得几何体的表面积.
解答:解:如图:

l与y轴、x轴交于A(0,8)B(6,0)两点
AB:y=-
x+8 与直线y=4x-8的交点为D
解之得,D(3,4)
线段AD、CD绕Y轴旋转一轴所围成几何体是两个圆锥组成
因为D(3,4),C(0,-8)
圆锥的底面半径是3
则AD=5,CD=3
,
AD为母线圆锥锥的侧面积:
(2πr)l=π×3×5=15π
CD为母线圆锥的侧面积:
(2πr)l=π×3×3
=9
π
围成几何体的表面积=3(3
+5)π.

l与y轴、x轴交于A(0,8)B(6,0)两点
AB:y=-
| 4 |
| 3 |
解之得,D(3,4)
线段AD、CD绕Y轴旋转一轴所围成几何体是两个圆锥组成
因为D(3,4),C(0,-8)
圆锥的底面半径是3
则AD=5,CD=3
| 17 |
AD为母线圆锥锥的侧面积:
| 1 |
| 2 |
CD为母线圆锥的侧面积:
| 1 |
| 2 |
| 17 |
| 17 |
围成几何体的表面积=3(3
| 17 |
点评:本题考查了两条直线相交的问题,先求出两直线的交点,再求出两个圆锥的侧面积,最后求出几何体的表面积.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
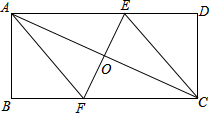 如图,在矩形ABCD中,对角线AC的垂直平分线分别交BC、AD于点F、E,垂足为O.
如图,在矩形ABCD中,对角线AC的垂直平分线分别交BC、AD于点F、E,垂足为O. 如图,在△ABC中,AB=AC,以AB边为直径作⊙O,交BC边于点D,过点D作,DF⊥AC于点F
如图,在△ABC中,AB=AC,以AB边为直径作⊙O,交BC边于点D,过点D作,DF⊥AC于点F 已知:如图,若AB∥DE,BC∥FE.求证:∠B+∠E=180°.
已知:如图,若AB∥DE,BC∥FE.求证:∠B+∠E=180°.