题目内容
20. 如图,BD⊥AC于点D,CE⊥AB于点E,AD=AE.求证:BE=CD.
如图,BD⊥AC于点D,CE⊥AB于点E,AD=AE.求证:BE=CD.
分析 要证明BE=CD,只要证明AB=AC即可,由条件可以求得△AEC和△ADB全等,从而可以证得结论.
解答 证明;∵BD⊥AC于点D,CE⊥AB于点E,
∴∠ADB=∠AEC=90°,
在△ADB和△AEC中,
$\left\{\begin{array}{l}{∠ADB=∠AEC}\\{AD=AE}\\{∠A=∠A}\end{array}\right.$
∴△ADB≌△AEC(ASA)
∴AB=AC,
又∵AD=AE,
∴BE=CD.
点评 本题考查全等三角形的判定和性质,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
10.下列调查中,适合采用全面调查(普查)方式的是( )
| A. | 了解某班同学“立定跳远”的成绩 | |
| B. | 了解全国中学生的心理健康状况 | |
| C. | 了解外地游客对我市旅游景点“磁器口”的满意程度 | |
| D. | 了解端午节期间重庆市场上的粽子质量情况 |
8.已知关于x的一元二次方程x2+mx-8=0的一个实数根为2,则另一实数根及m的值分别为( )
| A. | 4,-2 | B. | -4,-2 | C. | 4,2 | D. | -4,2 |
9.二次函数y=x2-2x+4化为y=a(x-h)2+k的形式,下列正确的是( )
| A. | y=(x-1)2+2 | B. | y=(x-1)2+3 | C. | y=(x-2)2+2 | D. | y=(x-2)2+4 |
 小聪有一块含有30°角的直角三角板,他想只利用量角器来测量较短直角边的长度,于是他采用如图的方法,小聪发现点A处的三角板读数为12cm,点B处的量角器的读数为74°,由此可知三角板的较短直角边的长度约为9cm.(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
小聪有一块含有30°角的直角三角板,他想只利用量角器来测量较短直角边的长度,于是他采用如图的方法,小聪发现点A处的三角板读数为12cm,点B处的量角器的读数为74°,由此可知三角板的较短直角边的长度约为9cm.(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75) 如图是由四个相同的小正方体组成的几何体,则这个几何体的主视图是( )
如图是由四个相同的小正方体组成的几何体,则这个几何体的主视图是( )



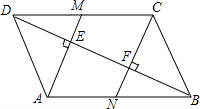 如图,?ABCD中,BD是它的一条对角线,过A、C两点作AE⊥BD,CF⊥BD,垂足分别为E、F,延长AE、CF分别交CD、AB于M、N.
如图,?ABCD中,BD是它的一条对角线,过A、C两点作AE⊥BD,CF⊥BD,垂足分别为E、F,延长AE、CF分别交CD、AB于M、N.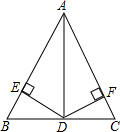 如图,在△ABC中,AD平分∠BAC,且BD=CD,DE⊥AB于点E,DF⊥AC于点F.
如图,在△ABC中,AD平分∠BAC,且BD=CD,DE⊥AB于点E,DF⊥AC于点F.