题目内容
4.x取哪些整数值时,不等式5x+2>3(x-1)与$\frac{1}{2}$x≤2-$\frac{3}{2}x$都成立?分析 根据题意分别求出每个不等式解集,根据口诀:大小小大中间找,确定两不等式解集的公共部分,即可得整数值.
解答 解:根据题意解不等式组$\left\{\begin{array}{l}{5x+2>3(x-1)}&{①}\\{\frac{1}{2}x≤2-\frac{3}{2}x}&{②}\end{array}\right.$,
解不等式①,得:x>-$\frac{5}{2}$,
解不等式②,得:x≤1,
∴-$\frac{5}{2}$<x≤1,
故满足条件的整数有-2、-1、0、1.
点评 本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
相关题目
19. 如图,从一张腰长为60cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的高为( )
如图,从一张腰长为60cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的高为( )
 如图,从一张腰长为60cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的高为( )
如图,从一张腰长为60cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的高为( )| A. | 10cm | B. | 15cm | C. | 10$\sqrt{3}$cm | D. | 20$\sqrt{2}$cm |
9.二次函数y=x2-2x+4化为y=a(x-h)2+k的形式,下列正确的是( )
| A. | y=(x-1)2+2 | B. | y=(x-1)2+3 | C. | y=(x-2)2+2 | D. | y=(x-2)2+4 |
 如图是由四个相同的小正方体组成的几何体,则这个几何体的主视图是( )
如图是由四个相同的小正方体组成的几何体,则这个几何体的主视图是( )



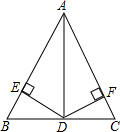 如图,在△ABC中,AD平分∠BAC,且BD=CD,DE⊥AB于点E,DF⊥AC于点F.
如图,在△ABC中,AD平分∠BAC,且BD=CD,DE⊥AB于点E,DF⊥AC于点F. 如图,已知⊙O,用尺规作⊙O的内接正四边形ABCD.(写出结论,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑)
如图,已知⊙O,用尺规作⊙O的内接正四边形ABCD.(写出结论,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑)
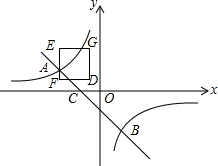 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于点A(-2,1),点B(1,n).
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于点A(-2,1),点B(1,n).