题目内容
 如图所示,已知直角梯形ABCD中,AD∥BC,∠C=∠D=90°,以AB为直径的⊙O与CD相切于P,若AD=m,BC=n,CD=a.求证:
如图所示,已知直角梯形ABCD中,AD∥BC,∠C=∠D=90°,以AB为直径的⊙O与CD相切于P,若AD=m,BC=n,CD=a.求证:(1)PC、PD是关于x的方程:x2-ax+mn=0的两根;
(2)a2=4mn.
考点:圆的综合题
专题:
分析:(1)首先利用切线的判定得出,△PAD∽△BPC进而求出PD•PC=m•n,即可得出答案;
(2)利用CD=PD+PC,PD=PC,CD=a,即可得出PC=
,则PC2=
,进而利用PC2=PC•PD,PD•PC=m•n,求出即可.
(2)利用CD=PD+PC,PD=PC,CD=a,即可得出PC=
| a |
| 2 |
| a2 |
| 4 |
解答: 证明:(1)连结OP.∵CD切⊙O于P,∴OP⊥CD,
证明:(1)连结OP.∵CD切⊙O于P,∴OP⊥CD,
∵AD⊥CD,BC⊥CD,∴AD∥OP∥BC.
又∵OA=OB,∴PC=PD,
∵CD=a,∴PC+PD=CD=a,
连结PA、PB,∵AB是⊙O 的直径,∴∠APB=90°,∴∠APD+∠BPC=90°,
∵∠D=90°,∴∠APD+∠PAD=90°,∴∠PAD=∠BPC,
又∵∠D=∠C=90°,∴△PAD∽△BPC,
∴
=
,∴PD•PC=AD•BC.
∵AD=m,BC=n,∴PD•PC=m•n,
故PC、PD是关于x的方程x2-ax+mn=0的两根.
(2)∵CD=PD+PC,PD=PC,CD=a,
∴PC=
,∴PC2=
,
又PC2=PC•PD,PD•PC=m•n,
∴
=mn,∴a2=4mn.
 证明:(1)连结OP.∵CD切⊙O于P,∴OP⊥CD,
证明:(1)连结OP.∵CD切⊙O于P,∴OP⊥CD,∵AD⊥CD,BC⊥CD,∴AD∥OP∥BC.
又∵OA=OB,∴PC=PD,
∵CD=a,∴PC+PD=CD=a,
连结PA、PB,∵AB是⊙O 的直径,∴∠APB=90°,∴∠APD+∠BPC=90°,
∵∠D=90°,∴∠APD+∠PAD=90°,∴∠PAD=∠BPC,
又∵∠D=∠C=90°,∴△PAD∽△BPC,
∴
| PD |
| BC |
| AD |
| PC |
∵AD=m,BC=n,∴PD•PC=m•n,
故PC、PD是关于x的方程x2-ax+mn=0的两根.
(2)∵CD=PD+PC,PD=PC,CD=a,
∴PC=
| a |
| 2 |
| a2 |
| 4 |
又PC2=PC•PD,PD•PC=m•n,
∴
| a2 |
| 4 |
点评:此题主要考查了圆的综合应用以及一元二次方程和相似三角形的判定与性质等知识,通过本题加深了这些知识的联系和沟通,提高了应用能力.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
 如图,在Rt△ABC中,∠C=90°,∠B=15°,DE垂直平分AB交BC于点E,BE=4,则AC长为( )
如图,在Rt△ABC中,∠C=90°,∠B=15°,DE垂直平分AB交BC于点E,BE=4,则AC长为( )| A、2 | B、3 |
| C、4 | D、2,3,4以外的值 |
 如图,直线y=-x+5分别与x轴、y轴交于A、B两点.
如图,直线y=-x+5分别与x轴、y轴交于A、B两点.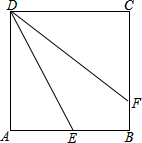 如图:已知在正方形ABCD中,E是边AB的中点,点F在BC上,且∠ADE=∠FDE.
如图:已知在正方形ABCD中,E是边AB的中点,点F在BC上,且∠ADE=∠FDE.