题目内容
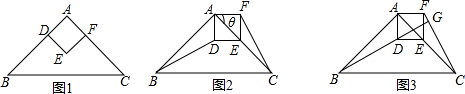
4.如图1,△ABC是等腰直角三角形,四边形ADEF是正方形,D、F分别在AB、AC边上,此时BD=CF,BD⊥CF成立.(1)当正方形ADEF绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
(2)当正方形ADEF绕点A逆时针旋转45°时,如图3,延长BD交CF于点G.
①求证:BD⊥CF;
②当AB=5,AD=$\sqrt{2}$时,求线段BG的长.
分析 (1)由△ABC是等腰直角三角形和ADEF是正方形得到判断△ABD≌△ACF的条件;
(2)由全等得到∠BGC=90°,利用勾股定理计算即可.
解答 解:(1)BD=CF成立.
理由:∵△ABC是等腰直角三角形,
∴AB=AC,
∵ADEF是正方形,
∴AD=AF,∠BAC=∠DAF,
∴∠BAC-∠DAC=∠DAF-∠DAC,
即∠BAD=∠CAF,
在△ABD和△ACF中
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAF}\\{AD=AF}\end{array}\right.$
∴△ABD≌△ACF,
∴BD=CF.
(2)①由(1)全等得:∠ABD=∠ACE,
∴∠GBC+∠GCB=∠GBC+∠ACF+∠ACB=(∠ABG+∠GBC)+∠ACB=45°+45°=90°,
∴∠BGC=90°,
∴BG⊥CF.
②如图3,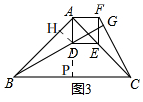
过D作DH⊥AB于H,AH=DH=AD÷$\sqrt{2}$=1,
∴BH=AB-AH=4,
∴BD=$\sqrt{B{H}^{2}+D{H}^{2}}$=$\sqrt{17}$,
延长AD交BC于P,
∴DP⊥BC,BP=$\frac{1}{2}$BC=$\frac{5\sqrt{2}}{2}$(AD平分∠BAC,AB=AC,等腰三角形三线合一)
由∠BGC=90°,
∴∠BPD=∠BGC,
∵∠DBP=∠CBG,
∴△DBP∽△CBG,
∴$\frac{BD}{BC}=\frac{BP}{BG}$,
∵BC=$\sqrt{2}$AB=5$\sqrt{2}$,
∴$\frac{\sqrt{17}}{5\sqrt{2}}=\frac{\frac{5\sqrt{2}}{2}}{BG}$
∴BG=$\frac{25\sqrt{17}}{17}$.
点评 此题是几何变换的综合题,主要考查等腰直角三角形和正方形的性质,平行线分线段成比例定理,判断出全等是解决本题的关键.

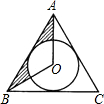 如图,已知等边三角形ABC的边长是6,⊙O是它的内切圆,则图中阴影部分的面积是3$\sqrt{3}$-π.
如图,已知等边三角形ABC的边长是6,⊙O是它的内切圆,则图中阴影部分的面积是3$\sqrt{3}$-π.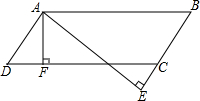 如图,过?ABCD的顶点A分别作AF⊥DC于F,AE⊥BC交BC的延长线于点E,若AE=3.5cm,AF=2.8cm,∠EAF=30°,则AB=7cm,AD=5.6cm.
如图,过?ABCD的顶点A分别作AF⊥DC于F,AE⊥BC交BC的延长线于点E,若AE=3.5cm,AF=2.8cm,∠EAF=30°,则AB=7cm,AD=5.6cm.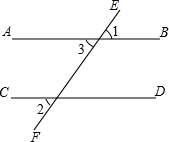 (1)如图,已知直线EF与AB、CD都相交,AB∥CD.
(1)如图,已知直线EF与AB、CD都相交,AB∥CD.