题目内容
如图，在等边△ABC中，AC=6，点D在边AC上，且AD=2，点E是AB边上的一动点，连接DE，以D为圆心，DE长为半径画弧，交BC于点F，连接EF，若ED=EF，那么BF长是（ ）| A、2 | B、3 | C、4 | D、6 |
考点：全等三角形的判定与性质,等边三角形的性质
专题：
分析：利用等边三角形性质结合全等三角形的判定方法得出△CDF≌△AED，进而求出即可．
解答：解：由题意可得：DF=DE，
∵DE=EF，
∴DE=DF=EF，
∴△DEF是等边三角形，
∴∠FDE=∠DEF=∠EFD=60°，
∴∠ADE+∠CDF=120°，∠ADE+∠AED=120°，
∴∠CDF=∠AED，
在△CDF和△AED中，
，
∴△CDF≌△AED（AAS），
∴CD=AE=4，
同理可得：△CDF≌△BFE，
则BF=DC=4．
故选：C．
∵DE=EF，
∴DE=DF=EF，
∴△DEF是等边三角形，
∴∠FDE=∠DEF=∠EFD=60°，
∴∠ADE+∠CDF=120°，∠ADE+∠AED=120°，
∴∠CDF=∠AED，
在△CDF和△AED中，
|
∴△CDF≌△AED（AAS），
∴CD=AE=4，
同理可得：△CDF≌△BFE，
则BF=DC=4．
故选：C．
点评：此题主要考查了全等三角形的判定与性质以及等边三角形的性质，得出△CDF≌△AED是解题关键．
练习册系列答案
相关题目
某商品的价格标签已丢失，售货员只知道“它的进价为80元，打七折售出后，仍可获利4元”，你认为销售员应标在标签上的价格为（ ）
| A、120元 | B、150元 |
| C、180元 | D、184元 |
如图，B、E、F、C在同一直线上，AF⊥BC于F，DE⊥BC于E，AB=DC，BE=CF，你认为AB平行于CD吗？说说你的理由．
如图，在Rt△ABC中，AB=AC，D，E是斜边BC上两点，且∠DAE=45°，将△ADC绕点A顺时针旋转90°后，得到△AFB，连接EF，下列结论：①△AED≌△AEF，②△ABE≌△ACD；③BE+DC=DE；④BE2+DC2=DE2，其中正确的是
如图，已知AB=AC，AD=AE，DB与CE相交于O．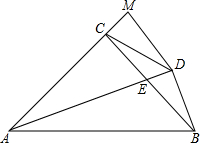
如图，在△ABC中，AC=BC，∠ACB=90°，AE平分∠BAC交BC于E，BD⊥AE于D，DM⊥AC交AC的延长线于M，连接CD．下列结论：
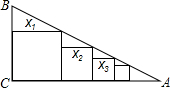已知Rt△ABC中，∠C=90°，BC=1，AC=4，如图把边长分别为x1，x2，x3，…，xn的n个正方形依次放入△ABC中，则第2015个正方形的边长为