题目内容
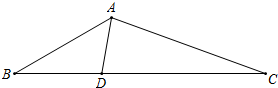 如图,在△ABC中,点D在BC上,AC=CD,∠B=30°,∠ADB=100°.
如图,在△ABC中,点D在BC上,AC=CD,∠B=30°,∠ADB=100°.(1)作AB的垂直平分线EF,分别交BC、AB于E、F(不写作法,保留作图痕迹);
(2)连结AE,求∠C与∠AED的大小.
考点:作图—基本作图,线段垂直平分线的性质
专题:
分析:(1)根据垂直平分线的作法作图;
(2)根据垂直平分线的性质和等腰三角形的性质解答.
(2)根据垂直平分线的性质和等腰三角形的性质解答.
解答: 解:(1)如图;
解:(1)如图;
(2)∵∠ADB=100°,
∴∠ADC=80°,
∵AC=CD,
∴∠DAC=∠ADC=80°,
∴∠C=20°,
由(1)知,EF垂直平分AB,
∴AE=BE,
∴∠BAE=∠B=30°,
∴∠AED=60°
 解:(1)如图;
解:(1)如图; (2)∵∠ADB=100°,
∴∠ADC=80°,
∵AC=CD,
∴∠DAC=∠ADC=80°,
∴∠C=20°,
由(1)知,EF垂直平分AB,
∴AE=BE,
∴∠BAE=∠B=30°,
∴∠AED=60°
点评:本题考查了作图--基本作图、线段垂直平分线的性质,要灵活运用以上性质,与等腰三角形的性质结合解答.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
已知命题“关于x的方程bx+1=0必有解”,能说明这个命题是假命题的一个反例是( )
| A、b=-1 | B、b=2 |
| C、b=-2 | D、b=0 |
下列说法中
①方程x(x-2)=x-2的解是x=1;
②小明沿着坡度为1:2的山坡向上走了1000m,则他升高了200
m;
③若直角三角形的两边长为3和4,则第三边的长为5
④将抛物线y=-x2向左平移2个单位后,得到的抛物线的解析式是y=-(x-2)2.
正确的命题有( )
①方程x(x-2)=x-2的解是x=1;
②小明沿着坡度为1:2的山坡向上走了1000m,则他升高了200
| 5 |
③若直角三角形的两边长为3和4,则第三边的长为5
④将抛物线y=-x2向左平移2个单位后,得到的抛物线的解析式是y=-(x-2)2.
正确的命题有( )
| A、0个 | B、1个 | C、2个 | D、3个 |
在△ABC中,锐角A、B满足|sinA-
|+[cos(B-15°)-
]2=0,则△ABC是( )
| ||
| 2 |
| ||
| 2 |
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、无法确定 |
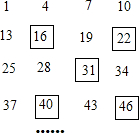 将一定规律的一组数1,4,7,10,13…排成如下表,并象如图一样对称框住其中五个数(阴影部分),请你仔细观察框住的五个数字规律,并回答下列问题:
将一定规律的一组数1,4,7,10,13…排成如下表,并象如图一样对称框住其中五个数(阴影部分),请你仔细观察框住的五个数字规律,并回答下列问题: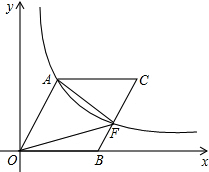 如图,O为坐标原点,点B在x轴的正半轴上,四边形OACB是平行四边形,sin∠AOB=
如图,O为坐标原点,点B在x轴的正半轴上,四边形OACB是平行四边形,sin∠AOB=