在我国古代数学著作中记载了一个有趣的问题.这个问题的意思是:有一个水池.截面是一个边长为12尺的正方形.在水池正中央有一根新生的芦苇.它高出水面2尺.如下图所示.如果把这根芦苇垂直拉向岸边.它的顶端恰好到达岸边的水面．那么水深多少?芦苇长为多少? 题目和参考答案——青夏教育精英家教网—

题目内容

16．

在我国古代数学著作《九章算术》中记载了一个有趣的问题，这个问题的意思是：有一个水池，截面是一个边长为12尺的正方形，在水池正中央有一根新生的芦苇，它高出水面2尺，如下图所示，如果把这根芦苇垂直拉向岸边，它的顶端恰好到达岸边的水面．那么水深多少？芦苇长为多少？

分析找到题中的直角三角形，设水深为x尺，根据勾股定理解答即可．

解答．解：设水深为x尺，则芦苇长为（x+2）尺，
根据勾股定理得：x²+（$\frac{12}{2}$）²=（x+2）²，
解得：x=8，
芦苇的长度=x+2=8+2=10（尺），
答：水池深8尺，芦苇长10尺．

点评本题考查勾股定理的应用．要善于观察题目的信息，由勾股定理得出方程是解决问题的关键．

练习册系列答案

相关题目

6．已知二次函数y=ax²，下列说法正确的是（　　）

	A．	当a＞0，x≠0时，y总取负值
	B．	当a＜0，x＜0时，y随x的增大而减小
	C．	当a＜0时，函数图象有最低点，y有最小值
	D．	当a＞0，x＞0时，图象在第一象限

7．观察下列算式，寻找规律，理由规律解答后面的问题：
1×3+1=4=2²，2×4+1=9=3²，3×5+1=16=4²，4×6+1=25=5²，…，
①请按上述规律填写：7×9+1=64=8²；
可知：若n为正整数，则n×（n+2）+1=（n+1）²．
②请你用找到的规律计算：（1+$\frac{1}{1×3}$）×（1+$\frac{1}{2×4}$）×（1+$\frac{1}{3×5}$）×…×（1+$\frac{1}{9×11}$）．

11．$\frac{1}{64}$的算术平方根的倒数是8．

1．

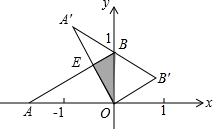如图，点A的坐标为（-$\sqrt{3}$，0），点B的坐标为（0，1），将△AOB绕原点O顺时针旋转60°到△A'OB'，A'B'恰好过点B，则B'的坐标为（$\frac{\sqrt{3}}{2}$，$\frac{1}{2}$），重叠部分△BOE的面积为$\frac{\sqrt{3}}{8}$．

8．计算：$\root{3}{1}$=1．

5．

在△ABC中，AB=AC，D、E分别在BC、AC上，AD=AE，∠CDE=20°，则∠BAD的度数为（　　）

试题分类