题目内容
11.两个正数满足a-b=2,ab=t-1,设p=(a+b)2,则P关于t的函数图象是( )| A. | 射线(不含端点) | B. | 线段(不含端点) | C. | 直线 | D. | 抛物线的一部分 |
分析 要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件,结合实际意义得到正确的结论.
解答 解:首先根据题意,消去字母a和b,得到S和t的关系式,
P=(a+b)2=(a-b)2+4ab=22+4(t-1)=4t,
然后根据题意,因为ab=t-1,所以t=ab+1,又因为ab>0,故t>1,①;
又因为P=(a+b)2>0,所以4t>0,所以t>1,②;
由①②得1<t.
故S关于t的函数图象是一条不含端点的射线.
故选A.
点评 本题考查了有自变量取值范围的函数的图象,关键是根据函数图象的性质和图象上的数据分析.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
1.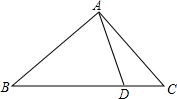 如图,D是△ABC一边BC上一点,连接AD,使△ABC∽△DBA的条件是( )
如图,D是△ABC一边BC上一点,连接AD,使△ABC∽△DBA的条件是( )
 如图,D是△ABC一边BC上一点,连接AD,使△ABC∽△DBA的条件是( )
如图,D是△ABC一边BC上一点,连接AD,使△ABC∽△DBA的条件是( )| A. | AC:BC=AD:BD | B. | AC:BC=AB:AD | C. | AB2=CD•BC | D. | AB2=BD•BC |
16.设二次函数y1=a(x-x1)(x-x2)(a≠0,x1≠x2)的图象与一次函数y2=dx+e(d≠0)的图象交于点(x1,0),若函数y=y1+y2的图象与x轴仅有一个交点,则( )
| A. | a(x1-x2)=d | B. | a(x2-x1)=d | C. | a(x1-x2)2=d | D. | a(x1+x2)2=d |
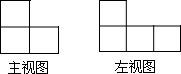 如图是由大小相同的小正方体组成的简单几何体的主视图和左视图,那么组成这个几何体的小正方体的个数最多为( )
如图是由大小相同的小正方体组成的简单几何体的主视图和左视图,那么组成这个几何体的小正方体的个数最多为( )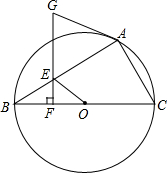 如图,已知,⊙O为△ABC的外接圆,BC为直径,点E在AB边上,过点E作EF⊥BC,延长FE交⊙O的切线AG于点G.
如图,已知,⊙O为△ABC的外接圆,BC为直径,点E在AB边上,过点E作EF⊥BC,延长FE交⊙O的切线AG于点G.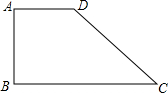 如图,直角梯形ABCD是一机器零件的横断面,已知DC=20cm,BC=40cm,∠DCB=30°,求AD的长为40-10$\sqrt{3}$cm.
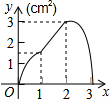
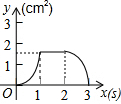
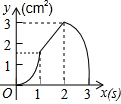
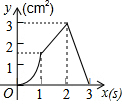
如图,直角梯形ABCD是一机器零件的横断面,已知DC=20cm,BC=40cm,∠DCB=30°,求AD的长为40-10$\sqrt{3}$cm.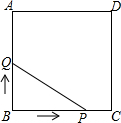 如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC-CD-DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )
如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC-CD-DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )