题目内容
已知0≤x≤1时,函数f(x)=x2-ax+a2的最小值为m.
(1)求m的值;(用含a的式子表示)
(2)求m的最大值.
(1)求m的值;(用含a的式子表示)
(2)求m的最大值.
考点:二次函数的最值
专题:
分析:(1)先配方得到f(x)=(x-
)2+
a2,则抛物线的对称轴为直线x=
,而抛物线开口向上,根据二次函数的性质讨论:当0≤
≤1时,m=
a2;当
≤0时,m=f(0)=a2;当
≥1,m=f(1)=a2-a+1;
(2)分段求最大值:当0≤a≤2,对于m=
a2,m的最大值为3;当a≤0,m没有最大值;当a≥2,m=a2-a+1=(a-
)2+
,a=2时,m有最大值3.
| a |
| 2 |
| 3 |
| 4 |
| a |
| 2 |
| a |
| 2 |
| 3 |
| 4 |
| a |
| 2 |
| a |
| 2 |
(2)分段求最大值:当0≤a≤2,对于m=
| 3 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
解答:解:(1)f(x)=x2-ax+a2
=(x-
)2+
a2,
抛物线的对称轴为直线x=
,抛物线开口向上,
当0≤
≤1时,即0≤a≤2,m=
a2;
当
≤0时,即a≤0,m=f(0)=a2;
当
≥1,即a≥2,m=f(1)=a2-a+1;
(2)当0≤
≤1时,即0≤a≤2,对于m=
a2,m的最大值为3;
当
≤0时,即a≤0,对于m=a2,m没有最大值;
当
≥1,即a≥2,m=a2-a+1=(a-
)2+
,a=2时,m有最大值3.
=(x-
| a |
| 2 |
| 3 |
| 4 |
抛物线的对称轴为直线x=
| a |
| 2 |
当0≤
| a |
| 2 |
| 3 |
| 4 |
当
| a |
| 2 |
当
| a |
| 2 |
(2)当0≤
| a |
| 2 |
| 3 |
| 4 |
当
| a |
| 2 |
当
| a |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
点评:本题考查了二次函数y=ax2+bx+c的最值:当a>0时,抛物线在对称轴左侧,y随x的增大而减少;在对称轴右侧,y随x的增大而增大,因为图象有最低点,所以函数有最小值,当x=-
时,y=
;当a<0时,抛物线在对称轴左侧,y随x的增大而增大;在对称轴右侧,y随x的增大而减少,因为图象有最高点,所以函数有最大值,当x=-
时,y=
.
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| 4ac-b2 |
| 4a |

练习册系列答案
相关题目
下列选项中是同类项的是( )
| A、-1和0 |
| B、abc和ab |
| C、-x2y5和2x2y |
| D、-a5b和4a5 |
现今世界上较先进的计算机显卡每秒可绘制出27000000个三角形,且显示逼真,用科学记数法表示这种显卡每秒绘制出三角形个数( )
| A、27×106 |
| B、0.27×108 |
| C、2.7×107 |
| D、270×105 |
 如图,点D、E在△ABC的边BC上,AD=AE,BD=EC,证明:△ABC是等腰三角形.
如图,点D、E在△ABC的边BC上,AD=AE,BD=EC,证明:△ABC是等腰三角形.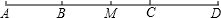 如图,已知B、C两点把线段AD分成2:4:3的三部分,M是AD的中点,若CD=6,求:
如图,已知B、C两点把线段AD分成2:4:3的三部分,M是AD的中点,若CD=6,求: