Question

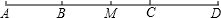如图，已知B、C两点把线段AD分成2：4：3的三部分，M是AD的中点，若CD=6，求：
（1）线段MC的长．
（2）AB：BM的值．

Answer 1

考点：两点间的距离

专题：

分析：（1）根据比例的性质，可得线段AB、线段BC的长，根据线段的和差，可得线段AD的长，根据线段中点的性质，可得MD的长，根据线段的和差，可得答案；
（2）根据线段中点的性质，可得AM的长，根据线段的和差，可得BM的长，根据比的意义，可得答案．

解答：解：（1）由AB：BC：CD=2：4：3，CD=6，得
AB=4，BC=8．
由线段的和差，得
AD=AB+BC+CD=4+8+6=18．
由线段中点的性质，得
AM=MD=

1

2

AD=9．
由线段的和差，得
MC=MD-CD=9-6=3；
（2）由线段的和差，得
BM=AM-AB=9-4=5．
由比的意义，得
AB：BM=4：5．

点评：本题考查了两点间的距离，利用了比例的性质，线段的和差，线段中点的性质．