题目内容
6.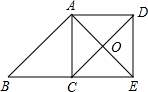 如图,?ABCD中,O为CD的中点,连接AO并延长,交BC延长线于E,连接AC,DE.
如图,?ABCD中,O为CD的中点,连接AO并延长,交BC延长线于E,连接AC,DE.(1)求证:四边形ACED为平行四边形;
(2)当∠B=∠AEB=45°时,四边形ACED为正方形,并证明.
分析 (1)根据平行四边形的性质求出AD=BC,AD∥BC,求出∠DAO=∠CEO,根据全等三角形的判定得出△ADO≌△ECO,推出AO=OE,根据平行四边形的判定推出即可;
(2)根据平行四边形的性质求出BC=CE,求出AC=CE,∠ACB=∠ACE=90°,根据正方形的判定得出即可.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠DAO=∠CEO,
∵O为CD的中点,
∴DO=CO,
在△ADO和△ECO中
$\left\{\begin{array}{l}{∠DAO=∠CEO}\\{∠AOD=∠COE}\\{DO=OC}\end{array}\right.$
∴△ADO≌△ECO,
∴AO=OE,
∵DO=OC,
∴四边形ACED为平行四边形;
(2)当∠B=∠AEB=45°时,四边形ACED为正方形,
证明:∵四边形ACED、四边形ABCD为平行四边形,
∴AD=BC,AD=CE,
∴BC=CE,
∵∠ABE=∠AEB=45°,
∴AB=AE,∠BAE=90°,
∴AC⊥BE,AC=CE,
∴∠ACB=∠ACE=90°,
∴四边形ACED是正方形,
即当∠B=∠AEB=45°时,四边形ACED为正方形,
故答案为:45°.
点评 本题考查了全等三角形的性质和判定,平行线的性质,平行四边形的性质和判定,正方形的判定,直角三角形的性质,等腰三角形的性质的应用,能综合运用性质进行推理是解此题的关键.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
1.等边三角形的边心距、半径、边长之比为( )
| A. | 1:$\sqrt{3}$:2 | B. | 1:2:$\sqrt{3}$ | C. | 1:2$\sqrt{3}$:2 | D. | 1:2:2$\sqrt{3}$ |
15.若两位数$\overline{ab}$是质数,交换数字后得到的两位数$\overline{ba}$也是质数,则称$\overline{ab}$为绝对质数,在大于11的两位数中绝对质数有( )个.
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
7.已知关于x的二次三项式4x2-mx+25是完全平方式,则常数m的值为( )
| A. | 10 | B. | ±10 | C. | -20 | D. | ±20 |
 如图,BE平分∠ABD,CF平分∠ACD,BE,CF相交于点G,若∠BDC=150°,∠BGC=95°,求∠A.
如图,BE平分∠ABD,CF平分∠ACD,BE,CF相交于点G,若∠BDC=150°,∠BGC=95°,求∠A.