题目内容
7．$\sqrt{5}$的整数部分为m，小数部分是n，则（$\sqrt{5}$+m）•n的值为（ ）| A． | 0 | B． | 1 | C． | $\sqrt{5}$+1 | D． | $\sqrt{5}$-1 |
分析 先估算无理数的范围，求出m、n的值，再代入求出即可．
解答 解：∵2＜$\sqrt{5}$＜3，
∴m=2，n=$\sqrt{5}$-2，
∴（$\sqrt{5}$+m）•n
=（$\sqrt{5}$+2）（$\sqrt{5}$-2）
=1，
故选B．
点评 本题考查了估算无理数的大小的应用，能求出m、n的值是解此题的关键．
练习册系列答案
相关题目
如图，花边上正三角形的内切圆半径1cm，如果这条花边中有100个圆和100个正三角形，算一算这条花边的总长度．
如图，在Rt△ABC中，∠C=90°，AB的垂直平分线交BC边于点E．连接AE，若∠B=15°，则∠EAC=60°．
如图，数轴上A、B两点对应的数分别为6和10，点P从原点O出发，以每秒3个单位长度的速度沿数轴正方向运动，同时点Q从点A出发，以每秒1个单位长度的速度沿数轴正方向运动．设运动时间为t秒．
19．
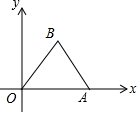如图在平面直角坐标系中，等边三角形OAB的顶点A在x轴上，顶点B在第一象限，若OA=2，则点B关于原点的对称点坐标为（ ）
如图在平面直角坐标系中，等边三角形OAB的顶点A在x轴上，顶点B在第一象限，若OA=2，则点B关于原点的对称点坐标为（ ）| A． | （1，$\sqrt{3}$） | B． | （$\sqrt{3}$，1） | C． | （-1，-$\sqrt{3}$） | D． | （-$\sqrt{3}$，-1） |
17．内角和为720?的多边形是（ ）
| A． |  | B． |  | C． |  | D． |  |