题目内容
已知函数y=(m+1)xm2+2m是关于x的二次函数.求:
(1)满足条件的m的值;
(2)m为何值时,抛物线有最低点?求出这个最低点,这时当x为何值时,y随x的增大而增大?
(3)m为何值时,函数有最大值?最大值是多少?这时当x为何值时,y随x的增大而减小?
(1)满足条件的m的值;
(2)m为何值时,抛物线有最低点?求出这个最低点,这时当x为何值时,y随x的增大而增大?
(3)m为何值时,函数有最大值?最大值是多少?这时当x为何值时,y随x的增大而减小?
考点:二次函数的最值,二次函数的定义
专题:
分析:(1)根据二次函数的定义求出m的值即可解决问题.
(2)运用当二次项系数大于0时,抛物线开口向上,图象有最低点;在对称轴的右侧y随x的增大而增大.
(3)运用当二次项系数小于0时,抛物线开口向下,图象有最高点;在对称轴的右侧y随x的增大而减小.
(2)运用当二次项系数大于0时,抛物线开口向上,图象有最低点;在对称轴的右侧y随x的增大而增大.
(3)运用当二次项系数小于0时,抛物线开口向下,图象有最高点;在对称轴的右侧y随x的增大而减小.
解答:解:(1)∵函数y=(m+1)xm2+2m是关于x的二次函数,
∴m2+2m=2,m+1≠0,
解得:m=-1±
.
(2)∵m=-1±
,
∴m+1=
或-
,
当m+1=
时,抛物线有最低点,该点坐标为(0,0);
当x>0时,y随x的增大而增大.
(3)当m+1=-
,
函数有最大值,最大值是0;
当x>0时,y随x的增大而减小.
∴m2+2m=2,m+1≠0,
解得:m=-1±
| 3 |
(2)∵m=-1±
| 3 |
∴m+1=
| 3 |
| 3 |
当m+1=
| 3 |
当x>0时,y随x的增大而增大.
(3)当m+1=-
| 3 |
函数有最大值,最大值是0;
当x>0时,y随x的增大而减小.
点评:该题主要考查了二次函数的定义及其性质的应用问题;牢固掌握定义及其性质是解题的关键.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
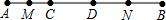 如图,C、D是线段AB上的两个点,CD=3cm,M是AC的中点,N是DB的中点,MN=5.4cm,那么线段AB的长等于( )
如图,C、D是线段AB上的两个点,CD=3cm,M是AC的中点,N是DB的中点,MN=5.4cm,那么线段AB的长等于( )| A、7.6cm | B、7.8cm |
| C、8cm | D、8.2cm |
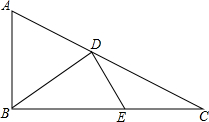 如图,△ABC中,∠ABC=90°,BC=2AB=4,D是AC上一动点,E是BC上一动点,则当BD+DE的值最小时,CE的长为
如图,△ABC中,∠ABC=90°,BC=2AB=4,D是AC上一动点,E是BC上一动点,则当BD+DE的值最小时,CE的长为