题目内容
18.在平面直角坐标系中,如果点P的纵坐标是横坐标的二倍,则称点P为“诚信点”,例如点(1,2),(-2,-4),($\sqrt{2}$,2$\sqrt{2}$),…都是“诚信点”,显然“诚信点”有无数个(1)若点P(m,6)是反比例函数y=$\frac{n}{x}$(n为常数,n≠0)的图象上的“诚信点”,求这个反比例函数的解析式
(2)函数y=2px+q(p,q为常数)的图象上存在“诚信点”吗?若存在,请求出“诚信点”的坐标,若不存在,说明理由
(3)若二次函数y=ax2+bx+1(a,b是常数,a>0)的图象上有且只有一个“诚信点”,令t=b2+4a,当-2<b<2时,试求t的取值范围.
分析 (1)根据“诚信点”的定义直接列出方程求解得出m,再用待定系数法求出反比例函数的解析式;
(2)先假设存在“诚信点”设出此点的坐标为(m,2m),根据“诚信点”的定义得出2m(p-1)=-q,然后分情况讨论即可;
(3)先设出“诚信点”的坐标为(m,2m),然后代入函数解析式中得出am2+(b-2)m+1=0,由于只有一个“诚信点”,即可得出△=(b-2)2-4a=0,即:(b-2)2=4a,即可用b表示出t,最后用b的范围即可得出结论.
解答 解:(1)∵点P(m,6)是“诚信点”,
∴2m=6,
∴m=3,
∴P(3,6),
∵点P(3,6)是反比例函数y=$\frac{n}{x}$(n为常数,n≠0)的图象上,
∴n=3×6=18,
∴反比例函数的解析式为y=$\frac{18}{x}$;
(2)假设函数y=2px+q(p,q为常数)的图象上存在“诚信点”,
设此点坐标为(m,2m),
∴2mp+q=2m,
∴2m(p-1)=-q,
∵p,q为常数,
∴①当p-1=0时,即p=1时,q=0,此时函数y=2x图象上的点全部是“诚信点”,
②当p-1≠0时,即p≠1时,
Ⅰ、当p=0时,此时函数为y=q,“诚信点”为($\frac{q}{2}$,q),
Ⅱ、当p≠0时,m=-$\frac{q}{2(p-1)}$,
∴“诚信点”为(-$\frac{q}{2(p-1)}$,-$\frac{q}{p-1}$).
(3)设二次函数y=ax2+bx+1(a,b是常数,a>0)的图象上的“诚信点”的坐标为(m,2m),
∴am2+bm+1=2m,
∴am2+(b-2)m+1=0,
∵二次函数y=ax2+bx+1(a,b是常数,a>0)的图象上有且只有一个“诚信点”,
∴am2+(b-2)m+1=0有两个相等的实数根,
∴△=(b-2)2-4a=0,
∴(b-2)2=4a,
∴t=b2+4a=b2+(b-2)2=2(b-1)2+2,
∵-2<b<2,
∴-3<b-1<1,
∴0<(b-1)2<9,
∴2<2(b-1)2+2<20,
∴2<t<20,
即:t的取值范围为2<t<20.
点评 此题是二次函数综合题,主要考查了新定义,待定系数法,一元二次方程的根的判别式等知识点;解本题的关键是理解“诚信点”的定义.

| A. | $\frac{x^2}{x^6}=\frac{1}{x^3}$ | B. | $\frac{{a}^{2}-{b}^{2}}{a-b}$=a+b | ||
| C. | $\frac{a+1}{{a}^{2}+1}$=$\frac{1}{a+1}$ | D. | $\frac{x+1}{{x}^{2}-2x+1}$=$\frac{1}{x+1}$ |
| A. | 5 | B. | $\frac{1}{5}$ | C. | -5 | D. | -$\frac{1}{5}$ |
| A. | 赚了 | B. | 赔了 | C. | 不赔不赚 | D. | 不能确定或赚 |

| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | 2 |
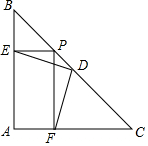 如图,已知在△ABC中,∠A=90°,AB=AC,D是BC的中点,P是BC上任意一点,且PE⊥AB于E,PF⊥AC于F,求证:DE=DF.
如图,已知在△ABC中,∠A=90°,AB=AC,D是BC的中点,P是BC上任意一点,且PE⊥AB于E,PF⊥AC于F,求证:DE=DF.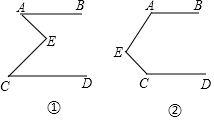 在图1和图2中,AB∥CD,你能说明∠A,∠E,∠C之间的数量关系吗?
在图1和图2中,AB∥CD,你能说明∠A,∠E,∠C之间的数量关系吗? 如图,四边形ABCD是⊙O的外切四边形,且AD=2,AB=3,BC=5,则CD=4.
如图,四边形ABCD是⊙O的外切四边形,且AD=2,AB=3,BC=5,则CD=4.