题目内容
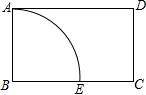 如图,在矩形ABCD中,AB=3,AD=6,以点B为圆心,BA长为半径画圆弧交BC于点E,点P在弧AE上,过点P作弧AE的切线,分别交AD、BC于点M、N,若MN恰好平分矩形ABCD的面积,则切线MN的长为
如图,在矩形ABCD中,AB=3,AD=6,以点B为圆心,BA长为半径画圆弧交BC于点E,点P在弧AE上,过点P作弧AE的切线,分别交AD、BC于点M、N,若MN恰好平分矩形ABCD的面积,则切线MN的长为考点:切线的性质,矩形的性质
专题:
分析:根据题意过BD的中点O弧AE的切线有两条,①E点就是P点,此时MN=EF=3,②根据切线长定理和勾股定理即可求得MN.
解答:
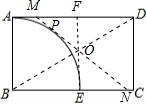 解:①连接BD,过O点作弧AE的切线,则MN恰好平分矩形ABCD的面积,
解:①连接BD,过O点作弧AE的切线,则MN恰好平分矩形ABCD的面积,
∵过O、E两点的直线正好是弧AE的切线,切点为E,
∴EF的长就是MN的长,
∵AB=3,
∴EF=3,
∴MN=EF=3;
②过O点作弧AE的另一条切线MN,切点为P,
∵AB是圆的半径,且AD⊥AB,
∴AD是圆B的切线,
∴AM=PM,OP=OE,
∵OE=OF=
CD=
AB=
,
∴OP=
,
设AM=x,则MP=x,MF=3-x,
在RT△MFO中,(3-x)2+(
)2=(
+x)2,
解得,x=1,
∴MF=3-1=2,
∴OM=
=
,
∴MN=2OM=5,
综上,切线MN的长为3或5.
故答案为3或5.
 解:①连接BD,过O点作弧AE的切线,则MN恰好平分矩形ABCD的面积,
解:①连接BD,过O点作弧AE的切线,则MN恰好平分矩形ABCD的面积,∵过O、E两点的直线正好是弧AE的切线,切点为E,
∴EF的长就是MN的长,
∵AB=3,
∴EF=3,
∴MN=EF=3;
②过O点作弧AE的另一条切线MN,切点为P,
∵AB是圆的半径,且AD⊥AB,
∴AD是圆B的切线,
∴AM=PM,OP=OE,
∵OE=OF=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∴OP=
| 3 |
| 2 |
设AM=x,则MP=x,MF=3-x,
在RT△MFO中,(3-x)2+(
| 3 |
| 2 |
| 3 |
| 2 |
解得,x=1,
∴MF=3-1=2,
∴OM=
| MF2+OF2 |
| 5 |
| 2 |
∴MN=2OM=5,
综上,切线MN的长为3或5.
故答案为3或5.
点评:本题考查了切线的判定和性质,矩形的性质,勾股定理的应用以及切线长定理的应用等,过O点可以作两条切线是本题的重点.

练习册系列答案
相关题目
一个负整数a,其倒数
与相反数-a相比较,正确的是( )
| 1 |
| a |
A、
| ||
B、
| ||
C、
| ||
| D、无法确定 |



 如图,直线l的函数关系式为y=kx+b-1,则3b与2k的大小关系是?
如图,直线l的函数关系式为y=kx+b-1,则3b与2k的大小关系是?