题目内容
观察下面的图形:它们是按一定规律排列的,依照此规律,第6个图形共有 个▲.


考点:规律型:图形的变化类
专题:
分析:由题意可知:第1个图形有1个▲,第2个图形有1+3=4个▲,第3个图形有1+3+5=9个▲,第4个图形有1+3+5+7=16个▲,…由此得出第n个图形有1+3+5+…2n-1=n2个▲,进一步代入求得答案即可.
解答:
解:第1个图形有1个▲,
第2个图形有1+3=4个▲,
第3个图形有1+3+5=9个▲,
第4个图形有1+3+5+7=16个▲,
…
第n个图形有1+3+5+…2n-1=n2个▲,
所以第6个图形共有62=36个▲.
故答案为:36.
第2个图形有1+3=4个▲,
第3个图形有1+3+5=9个▲,
第4个图形有1+3+5+7=16个▲,
…
第n个图形有1+3+5+…2n-1=n2个▲,
所以第6个图形共有62=36个▲.
故答案为:36.
点评:本题考查了图形的变化规律,关键是通过归纳与总结,得到其中的规律,利用规律解决问题.

练习册系列答案
相关题目
小强出生于公元2000年,用+2000年表示,那么孔子出生于公元前551年可表示为( )
| A、-2551年 |
| B、-1449年 |
| C、551年 |
| D、-551年 |
 如图,数轴上A、C两点对应的实数分别是1和2
如图,数轴上A、C两点对应的实数分别是1和2| 3 |
A、
| ||
B、1+
| ||
C、
| ||
D、2
|
若
=
,则
=( )
| a |
| b |
| 3 |
| 4 |
| b |
| a-b |
| A、-4 | ||
| B、4 | ||
C、-
| ||
D、
|
 已知:如图,在△ABC中,BC∥x轴,点A的坐标是(-4,3),点B的坐标是(-3,1)
已知:如图,在△ABC中,BC∥x轴,点A的坐标是(-4,3),点B的坐标是(-3,1) 如图,△ABC内接于⊙O,OD⊥BC于点D,∠A=55°,则∠OCD的度数是
如图,△ABC内接于⊙O,OD⊥BC于点D,∠A=55°,则∠OCD的度数是 用5个大小相同的小长方形拼成了如图所示的大长方形,若大长方形的周长是14,则每个小长方形的周长是
用5个大小相同的小长方形拼成了如图所示的大长方形,若大长方形的周长是14,则每个小长方形的周长是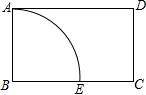 如图,在矩形ABCD中,AB=3,AD=6,以点B为圆心,BA长为半径画圆弧交BC于点E,点P在弧AE上,过点P作弧AE的切线,分别交AD、BC于点M、N,若MN恰好平分矩形ABCD的面积,则切线MN的长为
如图,在矩形ABCD中,AB=3,AD=6,以点B为圆心,BA长为半径画圆弧交BC于点E,点P在弧AE上,过点P作弧AE的切线,分别交AD、BC于点M、N,若MN恰好平分矩形ABCD的面积,则切线MN的长为