题目内容
四边形ABCD是对角线互相平分的四边形，请你添加一个适当的条件 ，使四边形ABCD成为菱形．
考点：菱形的判定
专题：
分析：添加AB=BC，首先根据对角线互相平分的四边形是平行四边形可得四边形ABCD是平行四边形，再根据邻边相等的平行四边形是菱形可得四边形ABCD是菱形．
解答：
解：添加AB=BC，
∵四边形ABCD是对角线互相平分的四边形，
∴四边形ABCD是平行四边形，
∵AB=BC，
∴四边形ABCD是菱形．
故答案为：AB=BC．
∵四边形ABCD是对角线互相平分的四边形，
∴四边形ABCD是平行四边形，
∵AB=BC，
∴四边形ABCD是菱形．
故答案为：AB=BC．
点评：此题主要考查了菱形的判定，关键是掌握邻边相等的平行四边形是菱形．
练习册系列答案
优等生题库系列答案
53天天练系列答案
相关题目
用5个大小相同的小长方形拼成了如图所示的大长方形，若大长方形的周长是14，则每个小长方形的周长是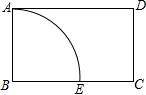
如图，在矩形ABCD中，AB=3，AD=6，以点B为圆心，BA长为半径画圆弧交BC于点E，点P在弧AE上，过点P作弧AE的切线，分别交AD、BC于点M、N，若MN恰好平分矩形ABCD的面积，则切线MN的长为
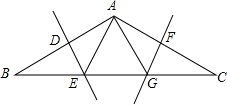如图，在△ABC中，AB=AC，∠BAC=120°，DE，FG分别是AB，AC的垂直平分线，且BC=12，则EG=在矩形ABCD中，E，F分别为AB，CD的中点，如果矩形ABCD∽矩形EFCB，那么它们的相似比为（ ）
A、
| ||||
| B、2 | ||||
C、
| ||||
D、
|
如图，在△ABC中，∠B=50°，∠AEC=80°，CE平分∠ACB，求∠A和∠BCD的度数．