题目内容
如图,用同样规格黑白两色的正方形瓷砖铺设矩形地面,观察下列图形并解答有关问题:
(1)在第n个图中,每一横行共有 块瓷砖,每一竖行共有 块瓷砖(均用含n的代数式表示);
(2)按上述方案,铺设这样的矩形地面共用了506块瓷砖,求此时n的值;
(3)是否存在黑、白瓷砖块数相等的情形?请通过计算说明.

(1)在第n个图中,每一横行共有
(2)按上述方案,铺设这样的矩形地面共用了506块瓷砖,求此时n的值;
(3)是否存在黑、白瓷砖块数相等的情形?请通过计算说明.
考点:规律型:图形的变化类
专题:
分析:(1)观察图形得出答案即可;
(2)求得总块数,联立方程求得n的数值即可;
(3)分别表示出第n个图中黑、白瓷砖块数,联立方程求得n的数值验证即可.
(2)求得总块数,联立方程求得n的数值即可;
(3)分别表示出第n个图中黑、白瓷砖块数,联立方程求得n的数值验证即可.
解答:
解:(1)每-横行有(n+3)块,每-竖列有(n+2)块.
(2)由题意,得(n+3)(n+2)=506,解之n1=20,n2=-25(舍去).
(3)当黑白砖块数相等时,有方程n(n+1)=(n2+5n+6)-n(n+1).
整理得n2-3n-6=0.
解之得n1=
,n2=
.
由于n1的值不是整数,n2的值是负数,故不存在黑砖白块数相等的情形.
(2)由题意,得(n+3)(n+2)=506,解之n1=20,n2=-25(舍去).
(3)当黑白砖块数相等时,有方程n(n+1)=(n2+5n+6)-n(n+1).
整理得n2-3n-6=0.
解之得n1=
3+
| ||
| 2 |
3-
| ||
| 2 |
由于n1的值不是整数,n2的值是负数,故不存在黑砖白块数相等的情形.
点评:此题考查图形的变化规律,找出图形之间的联系,得出运算的规律,利用规律解决问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
小强出生于公元2000年,用+2000年表示,那么孔子出生于公元前551年可表示为( )
| A、-2551年 |
| B、-1449年 |
| C、551年 |
| D、-551年 |
0.0045用科学记数法表示为( )
| A、4.5×103 |
| B、4.5×10-3 |
| C、4.5×10-4 |
| D、0.45×10-5 |

 已知:如图,在△ABC中,BC∥x轴,点A的坐标是(-4,3),点B的坐标是(-3,1)
已知:如图,在△ABC中,BC∥x轴,点A的坐标是(-4,3),点B的坐标是(-3,1) 如图,△ABC内接于⊙O,OD⊥BC于点D,∠A=55°,则∠OCD的度数是
如图,△ABC内接于⊙O,OD⊥BC于点D,∠A=55°,则∠OCD的度数是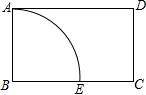 如图,在矩形ABCD中,AB=3,AD=6,以点B为圆心,BA长为半径画圆弧交BC于点E,点P在弧AE上,过点P作弧AE的切线,分别交AD、BC于点M、N,若MN恰好平分矩形ABCD的面积,则切线MN的长为
如图,在矩形ABCD中,AB=3,AD=6,以点B为圆心,BA长为半径画圆弧交BC于点E,点P在弧AE上,过点P作弧AE的切线,分别交AD、BC于点M、N,若MN恰好平分矩形ABCD的面积,则切线MN的长为