题目内容
5.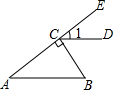 如图,BC⊥AE于点C,CD∥AB,∠B=55°,则∠1等于( )
如图,BC⊥AE于点C,CD∥AB,∠B=55°,则∠1等于( )| A. | 55° | B. | 45° | C. | 35° | D. | 25° |
分析 根据垂直的定义得到∠ACB=90°,得到∠BCE=90°,根据平行线的性质求出∠BCD=55°,计算即可.
解答 解:∵BC⊥AE,
∴∠ACB=90°,
∴∠BCE=90°,
∵CD∥AB,∠B=55°,
∴∠BCD=∠B=55°,
∴∠1=90°-55°=35°,
故选:C.
点评 本题考查的是平行线的性质和垂直的定义,两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.下列说法中正确的是( )
| A. | -a表示负数 | |
| B. | 多项式-3a2b+7a2b2-2ab+1是四次四项式 | |
| C. | 单项式-$\frac{2x{y}^{2}}{9}$的系数为-2 | |
| D. | 若|x|=-x,则x<0 |
5.下列不等式中,正确的是( )
| A. | m与4的差是负数,可表示为m-4<0 | B. | x不大于3可表示为x<3 | ||
| C. | a是负数可表示为a>0 | D. | x与2的和是非负数可表示为x+2>0 |
 在平面直角坐标系内按下列要求完成作图(不要求写作法,保留作图痕迹).
在平面直角坐标系内按下列要求完成作图(不要求写作法,保留作图痕迹).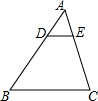 如图,在△ABC中,DE∥BC,$\frac{AD}{AB}$=$\frac{1}{3}$,BC=12,则DE的长是( )
如图,在△ABC中,DE∥BC,$\frac{AD}{AB}$=$\frac{1}{3}$,BC=12,则DE的长是( ) 如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于$\frac{1}{2}BF$长为半径画弧,两弧交于一点P,连
如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于$\frac{1}{2}BF$长为半径画弧,两弧交于一点P,连