题目内容
10. 如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于$\frac{1}{2}BF$长为半径画弧,两弧交于一点P,连
如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于$\frac{1}{2}BF$长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.
(1)四边形ABEF是菱形;(选填矩形、菱形、正方形、无法确定)(直接填写结果)
(2)AE,BF相交于点O,若四边形ABEF的周长为40,BF=10,则AE的长为10$\sqrt{3}$,∠ABC=120°.(直接填写结果)
分析 (1)先证明△AEB≌△AEF,推出∠EAB=∠EAF,由AD∥BC,推出∠EAF=∠AEB=∠EAB,得到BE=AB=AF,由此即可证明.
(2)根据菱形的性质首先证明△AOB是含有30°的直角三角形,由此即可解决问题.
解答 解:(1)在△AEB和△AEF中,
$\left\{\begin{array}{l}{AB=AF}\\{∠EAB=∠EAF}\\{AE=AE}\end{array}\right.$,
∴△AEB≌△AEF,
∴∠EAB=∠EAF,
∵AD∥BC,
∴∠EAF=∠AEB=∠EAB,
∴BE=AB=AF.
∵AF∥BE,
∴四边形ABEF是平行四边形
∵AB=AF,
∴四边形ABEF是菱形.
故答案为菱形.
(2)∵四边形ABEF是菱形,
∴AE⊥BF,BO=OF=5,∠ABO=∠EBO,
∵AB=10,
∴AB=2BO,∵∠AOB=90°
∴∠BA0=30°,∠ABO=60°,
∴AO=$\sqrt{3}$BO=5$\sqrt{3}$,∠ABC=2∠ABO=120°.
故答案为$10\sqrt{3}$,120.
点评 本题考查菱形的判定和性质、平行四边形的性质、作图-基本作图等知识,解题的关键是全等三角形的证明,想到利用特殊三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
1.已知△ABC的周长是l,BC=l-2AB,则下列直线一定为△ABC的对称轴的是( )
| A. | △ABC的边AB的垂直平分线 | B. | ∠ACB的平分线所在的直线 | ||
| C. | △ABC的边BC上的中线所在的直线 | D. | △ABC的边AC上的高所在的直线 |
5.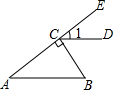 如图,BC⊥AE于点C,CD∥AB,∠B=55°,则∠1等于( )
如图,BC⊥AE于点C,CD∥AB,∠B=55°,则∠1等于( )
 如图,BC⊥AE于点C,CD∥AB,∠B=55°,则∠1等于( )
如图,BC⊥AE于点C,CD∥AB,∠B=55°,则∠1等于( )| A. | 55° | B. | 45° | C. | 35° | D. | 25° |
9.如果a>b,那么下列不等式中正确的是( )
| A. | a-b<0 | B. | a+3<b-3 | C. | ac2>bc2 | D. | 3-a<3-b |
